
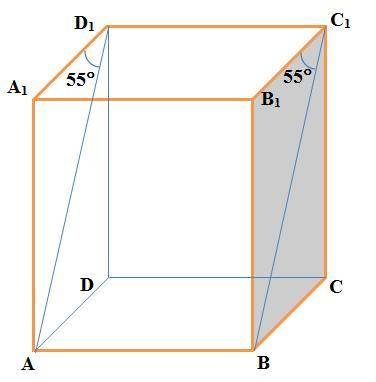
Угол между прямыми C₁B и AA₁ равен 35°
Объяснение:
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
В задаче C₁B и AA₁ являются скрещивающимися прямыми (см. рисунок). Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно, параллельными данным скрещивающимся прямым.
В силу этого, так как C₁B || D₁A, то угол между прямыми C₁B и AA₁ равен углу между прямыми D₁A и AA₁, то есть ∠A₁AD₁. В треугольнике ΔAA₁D₁:
∠AD₁A₁+∠D₁A₁A+∠A₁AD₁=180°.
Тогда, так как ∠AA₁D₁=90° и ∠AD₁A₁=55°, то ∠A₁AD₁=180°–90°–55°=35°.
Обозначим один катет как х, а другой как у.
Составим систему уравнений.
х^2+y^2=169...
x-y=7... x=7+y
Подставим.
(7+у)^2+y^2=169
49+14y+y^2+y^2-169=0
2y^2+14y-120=0
D=196-4*2*(-120)=196+960=1156 (34)
y1=(-14+34)/4=5
y2=(-14-34)/4=-12
Находим х.
х1-5=7
х1=12
х2+12=7
х2=-5
ответ: (12;5) и (-5;-12)