Утр-ку abc кут c=90 градусов,ab=13см bc=5см. знайти косинус кута b та тангенс кута a

👇

Увидеть ответ

Открыть все ответы

Ответ:

hjdbrvjt

27.11.2021

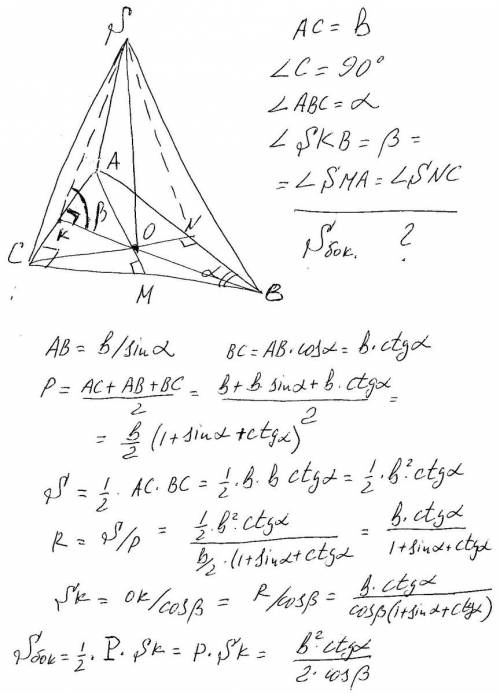
Позначимо вершину піраміди S, вершини трикутника в основі АВС, причому

кут С=90°

кут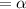 $А=\alpha$

BC=b

Кожна бічна грань нахилена до основи піраміди під кутом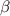 $\beta$ ., значить вершина піраміди проектується в центр О - вписаного кола. Нехай 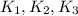K_1, K_2, K_3 точки дотику вписаного в трикутник АВС кола до сторін АВ, АС, ВС відповідно. Тоді

кут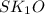 SK_1O = SK_2O = SK_3O = $\beta$

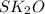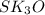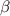
SO - висота піраміди,

за теоремою про три перпендикуляри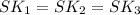 SK_1=SK_2=SK_3 - висоти трикутників (граней) ASB, ASC, BSC відповідно.

площа бічної поверхні =сумі площ бічних граней=сумі площ трикутників ASB, ASC, BSC

Площа трикутника дорівнює півдобутку сторони трикутника на висоту, проведену до цієї сторони.

За співвідношенями в трикутнику

BC=b,

tg A=BC/AC $AC=BC/tg A=BC*ctg A=b*ctg\alpha$

Зі співвідношень в прямокутних трикутних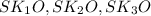 SK_1O, SK_2O, SK_3O маємо

$h=SK_1=SK_2=SK_3=\frac {r}{cos \beta}$

площа бічної поверхні дорівнює

$S=\frac {AB*SK_1+AC*SK_2+BC*SK_3}{2}=\frac {AB+BC+AC}{2}*h=\frac {pr}{cos \beta}=\frac {AC*BC}{2cos \beta}=\frac {b*b*ctg \alpha}{2cos \beta} =\frac {b^2*ctg\alpha}{2cos \beta}$

(Площа прямокутного трикутника= добутку півпериметра на радіус вписаного кола=півдобутку катетів)

Основою піраміди є прямокутний трикутник з гострим кутом α і катетом b, протилежним йому. кожна бічн

4,5(29 оценок)

Ответ:

Miraflores18

27.11.2021

Обозначим пирамиду АВСS(смотри рисунок). Поскольку все грани наклонены под одинаковым углом, то высота пирамиды опущенная из вершины S приходит в точку О-пересечение биссектрис, которая является центром вписанной окружности и её радиусы OK, OM,ON (рисунок условный-эти радиусы не являются продолжением биссектрис после точки О, они перпендикулярны сторонам). Продолжения биссектрис не показаны, чтобы не загромождать рисунок. Дальше -простая тригонометрия, радиус находим через площадь и полупериметр. Площадь боковой поверхности равна полвине периметра умноженное на апофему или полупериметр на апофему. ответ на рисунке.