Геометрическая фигура - множество точек, которое образует конечное количество линий. Основными геометрическими фигурами являются точка и прямая линия.
Геометрическое место точек, удаленных от заданной точки на заданное расстояние - окружность.
Геометрическое место точек, равноудаленных от сторон угла - биссектриса.
Геометрическое место точек, равноудаленных от концов отрезка - серединный перпендикуляр к отрезку.
Геометрическое место точек, удаленных от заданной прямой на заданное расстояние - прямая, параллельная заданной прямой.
Вообщем я немного упростила это решение
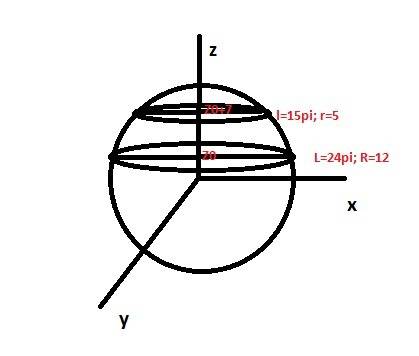
Пусть большее сечение лежит выше центра шара по оси Z , его радиус 12 и центр в точке (0;0;z0)
Тогда его уравнение будет x^2+y^2+z0^2=R^2
Здесь R радиус сферы. Так как радиус большего сечения 12(24pi/2pi), то уравнение большего круга
Будет 12^2+z0^2=R^2
Меньшее сечение x^2+y^2+(z0+7)^2==R^2; 25+z0^2+14z0+47=R^2
Вычитаю из первого второе , получу
119-17z0-49=0
-14z0=-70
Z0=5
Выходит большее сечение находится от центра шара по оси z на расстоянии 5, значит
R^2=5^2+12^2=169
R=13
S(cф)=4pi*13^2=676pi
Одна сторона их равна 3 см ( по стороне основания призмы).
Диагональ делит грань на два треугольника.
Причем отношение сторон в треугольнике позволяет предположить, что вторая сторона грани равна 4. ( Это «египетский» треугольник. Проверив по т. Пифагора, можно убедиться в этом).
Итак, высота призмы 4см, сторона основания - 3см
Площадь боковой поверхности равна произведению высоты на периметр основания ( но можно вычислить площадь одной грани и умножить на их количество, т .е. на 3).
S бок=3*3*4=24 см²
В основаниях призмы - два правильных треугольника. Площадь правильного треугольника находим по формуле:
S=(a² √3):4
S=9√3):4
S полн=24+2*9√3):4=24+(18√3):4 см²или (96+18√3):4 см²