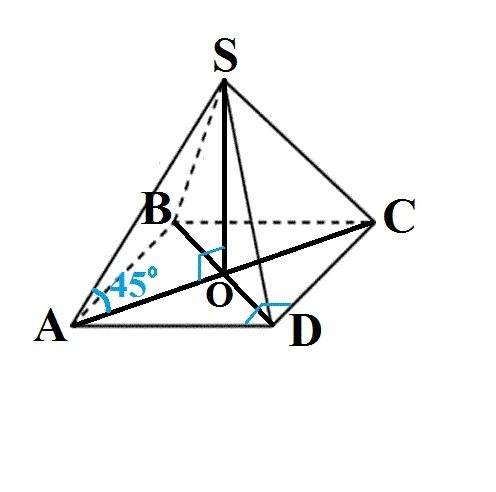
Т. к дана правильная четырехугольная пирамида, то в основании лежит квадрат со стороной 6 см, значит диагональ этого квадрата равна 6* корень из 2, а половина диагонали 3* корень из 2. Боковое ребро пирамиды наклонено к плоскости основания под углом 45 градусов, то прямоугольный треугольник, состоящий из высоты пирамиды и половины диагонали квадрата является равнобедренным. Значит высота пирамиды равна половине диагонали = 3* корень из 2. S осн=36см^2
V=1/3*S осн*h=1/3*36*3*корень из 2=36* корень из 2
Сечение amb, площадь которого надо найти - равнобедренный треугольник с основанием ab и боковыми сторонами am и bm. Основание нам дано - это сторона основания пирамиды, равная 8. Боковые грани - равные равнобедренные треугольники. Значит углы при вершинах граней равны 36°, равны и все углы при основании граней (180°-36°):2 = 72°.
В треугольнике asm <asm=36°(дано), <sam=36°(как половина угла sac=72°) и <amb=(180°-72°)=108°. Углы ams и amc смежные. Тогда <amc=180°-108°=72° и значит треугольник amc равнобедренный и am=ac=8. Но am=bm, а ac=ab. Значит сечение - правильный треугольник и его площадь равна:
Sabm = (√3/4)*a², где а - сторона треугольника.
Итак, Sabm = (√3/4)*64 = 16√3.