Величина углов для пропорционных чисел равна соответственно:
3, 4, 4, 5, 3, 5
90° 120° 120° 150° 90° 150°
Объяснение:
Сумма всех (внешних) углов многоугольника равна:
s = 180° × (n - 2), где n - количество сторон многоугольника.
В шестиугольнике 6 сторон, поэтому
s = 180° × (6 - 2) = 180° × 4 = 720°
Если сумма всех пропорционных чисел относится к сумме всех углов:
24 : 720°, тогда найдём соотношение всех данных нам пропорционных чисел к их углам через пропорции:
24 : 720°
3 : Х Х = (720° × 3) / 24 = 90°;
24 : 120°
4 : Х Х = (120° × 4) / 24 = 120°;
24 : 120°
5 : Х Х = (120° × 5) / 24 = 150°.
Поэтому: все углы, пропорционные числу 3 равны 90°
все углы, пропорционные числу 3 равны 1200°
все углы, пропорционные числу 3 равны 150°
Проверим: 90° + 120°+ 120° + 150° + 90° + 150° = 720°
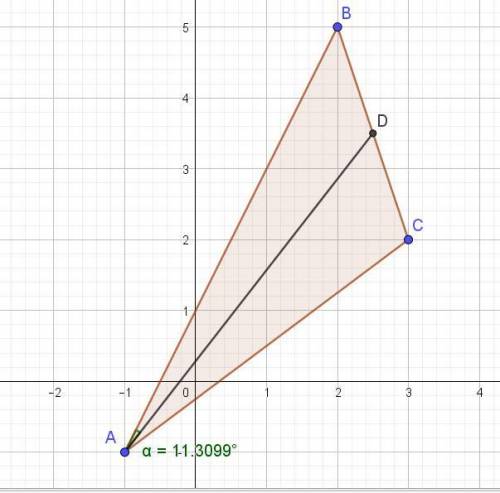
Даны координаты вершин треугольника ABCA: (− 1,−1), B( 2,5 ), C( 3,2 ).
Найти:
1) Уравнение линии BC ;
Вектор ВС = (3-2; 2-5)= (1; -3).
Уравнение ВС: (х - 2)/1 = (у - 5)/(-3) или в виде уравнения с угловым коэффициентом у = -3х + 11.
2) Уравнение высоты AK - это перпендикуляр к стороне ВС.
Тогда к(АК) = -*1/к(ВС) = -1/(-3) = 1/3.
Уравнение АК: у = (1/3)х + в.
Чтобы найти в подставим координаты точки А: -1 = (1/3)*(-1) + в, отсюда
в = -1 + (1/3) = (-2/3).
Уравнение АК: у = (1/3)х - (2/3).
3) Длину высоты AK ;
Это расстояние от точки А до прямой ВС.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = |A·Mx + B·My + C| /√(A² + B²).
Подставим в формулу данные:
d = |3·(-1) + 1·(-1) + (-11)|/ √32 + 12 = |-3 - 1 - 11| /√(9 + 1 ) =
= 15 /√10 = 3√10 /2 ≈ 4.743416.
4) Уравнение прямой (l), которая проходит через точку A параллельно прямой BC ;
У этой прямой угловой коэффициент равен такому у прямой ВС,
Уравнение: у = -3х + в. Подставим координаты точки А:
-1 = (-3)*(-1) + в, отсюда в = -1 - 3 = -4.
Уравнение: у = -3х - 4.
5) Уравнение медианы (AM ), проведенной через вершину A;
Находим координаты точки М как середину стороны ВС. B( 2,5 ), C( 3,2 )
М = (2,5; 3,5). Вектор АМ = (2,5-(-1); 3,5-(-1)) = (3,5; 4,5).
Уравнение АМ: (х + 1)/3,5 = (у + 1)/4,5 или с целыми коэффициентами
(х + 1)/7 = (у + 1)/9.
Уравнение АМ в общем виде 9х - 7у + 2 = 0.
6) Угол (φ), образованный медианой, проведенной из вершины A, и стороной AB;
Вектор АВ = (2-(-1); 5-(-1)) = (3; 6). Модуль равен √(9+36) = √45 = 3√5.
Вектор АМ = (7; 9). Модуль равен √(49+81) = √130.
cos φ = (3*7 + 6*9)/(3√5*√130) = 75/15√26 = 5√26/26 = 0,98058.
Угол φ = arc cos(5√26/26) = 0,1974 радиан или 11,30993 градуса.
7) Площадь треугольника ABC ;
S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 7,5 кв.ед.
8) Периметр треугольника ABC .
Периметр Р = 14,87048 .
Найти: АВ.
Решение:
С прямоугольного треугольника АСН (∠АНС = 90):
Определим ∠А:
sin ∠A = CH / AC =24/30 = 0.8 - (синус угла А это отношение противолежащего катета СН к гипотенузе АВ).
По таблице sin ∠A = 0.8, то ∠А = 53,1301
Теперь определяем боковую сторону
AB = (AC/2) / cos∠A = 15/cos53.1301 ≈ 25 (см).
ответ: 25 (см).