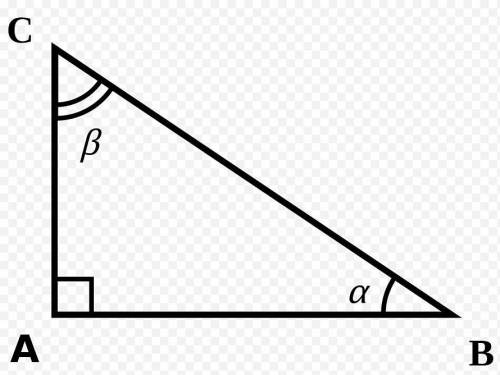
Дано:
ABC- прямокутний трикутник
СВ= 7 см
Кут В= 60°
Знайте: АС, АВ
Розв'язання
sin кута В= АС/СВ
АС= sin 60°* CB= 0,8660*7= приблизно 6 см
cos кута В= АВ/СВ
АВ= cos 60°* CB= 0,5*7=3,5 см
Відповідь: АС= 6 см, АВ= 3,5 см
180-90-60= 30° - Кут С
АВ=1/2 СВ (тому що напроти АВ є кут 30°, а за властивістю прямокутного трикутника, катет що лежить напроти кута 30° буде дорівнювати 1/2 гіпотенузи)
АВ= 1/2 СВ= 7:2= 3,5
Із трикутника АВС за теоремою Піфагора:
АС²= СВ²- АВ²= 7²- 3,5²= 49- 12,25= 36,75
АС= √36,75= приблизно 6 см
Відповідь: та же що і у першому варіанті
Уточнение:
Я не могу точно быть уверена в ответе, но эту задачу я делала по принципу, по которому мы решаем в классе
АВС - прямоугольный тр-ник, угол В прямой, АС - гипотенуза. ВМ - медиана.
Медиана делит сторону, к которой она проведена, пополам. Значит АМ = МС.
В прямоугольном тр-нике медиана, проведенная к гипотенузе, равна ее половине, т.е.
ВМ = ВМ = СМ = 10 см, тогда гипотенуза АС = 20 см.
Медиана ВМ делит прямой угол в отношении 1 : 2, значит
угол АВМ = 90 : 3 * 2 = 60 градусов
угол СВМ = 90 - 60 = 30 градусов.
Тр-ник АМВ - равнобедренный, поскольку АМ = ВМ, АВ - основание.
Углы при основании равны, т.е. угол МАВ = МВА = 60, тогда угол АМВ = 180 - 60 * 2 = 60.
Значит тр-ник АМВ равносторонний, АВ = 16 см.
Меньшая средняя линия параллельна меньшей стороне (АВ) и равна ее половине, т.е. 8 см.
В трапецию вписана окружность (О: 3)- центр О, радиус 3.
Найти КТ.
Решение. Площадь трапеции
Высота трапеции равна диаметру окружности. h=6
Значит a+b=108:3, a+b=36
По свойству окружности вписанной в четырехугольник суммы противоположных сторон такого четырехугольника равны между собой.
a+b=c+d, где с и d - ,боковые стороны трапеции и c=d/
Значит сумма оснований трапеции 36, боковые стороны трапеции 18
Проведем высоту ВR. По теореме Пифагора АR²=18²-6²=(18-6)(18+6)=12·24
AR=12√2.
Значит меньшее основание трапеции
ВС= (36-24√2)/2,
BC=18-12√2.
BC=9-6√2
AD= 18+12√2
AG=AD|2=9+6√2
Треугольники SBF и SAG подобны.
Из подобия: SB: SA= BF:AG
SB:(SB+18)=(9-6√2):(9+6√2)
SB=(54-36√2)|4√2
Из подобия треугольников SKE и SBF:
SB:SK=BF: KE
SK=SB+3
KE=SK·BF/SB
KТ=2КЕ=2·(9-4√2)/(9(3-2√2)²)