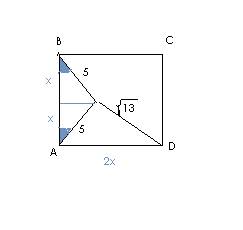
Втреугольнике авс через точку n, взятую на стороне вс, проведена прямая, пересекающая сторону ас и пересекающая в точке м продолжение стороны ва. найти отношение ва: ам, если известно, что данная прямая делит площадь треугольника авс в соотношении 4: 1 и вn=2nc.
BN*CK*AM/(NC*KA*MB) = 1;
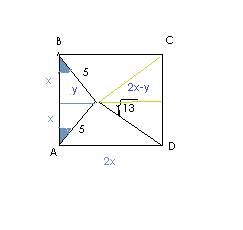
Если обозначить KC = p*AC; AM = q*BA; то
2*p*q/((1-p)*(1+q)) = 1; (1)
Треугольник CNK по условию имеет площадь 1/5 от площади ABC; (я считаю, что площадь BNKA в 4 раза БОЛЬШЕ площади CNK. Если наоборот, то положение точки K не может соответствовать условию - она будет вне треугольника.)
По условию NC = BC/3; поэтому расстояние от N до AC составляет 1/3 расстояния от B до AC. Отсюда (площадь CNK) = p*(1/3)*(площадь ABC); или
p/3 = 1/5; p = 3/5; p/(1 - p) = 3/2; если подставить это в (1)
q/(1 + q) = 1/3; q = 1/2;
То есть AM = BA/2;
Доказательство теоремы Менелая необыкновенно простое. Если провести какую-то прямую вне треугольника, так, чтобы она пересекалась с прямой NM в точке D где-то вне треугольника, потом провести через три вершины прямые параллельно NM, которые пересекут эту прямую в точках A2; B2; C2; (ну, в смысле AA2 II BB2 II CC2 II MN, и напомню, точка К - тоже на MN)
то
(BN/NC)*(CK/KA)*(AM/MB) = (B2D/DC2)*(C2D/DA2)*(A2D/DB2) = 1;
это всё доказательство. С учетом "знака", то есть "направления" отрезка, пишут обычно -1; тут при составлении равенств важно не запутаться в отрезках :)))