доказано
Объяснение:
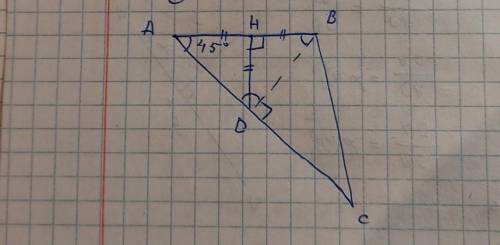
нарисуем треугольник АВС
где угол А =45°и нарисуем серединную высоты к стороне АВ
АН=НВ=НD потому что прямоугольный треугольник АНD равнобедренный
проведём линию DB
линия DB перпендикулярна к стороне DC , потому что углы ADH и HDB по 45°,что значит угол BDC 180°-45°-45°= 90°
из этого выходит что треугольник BDC прямоугольный
сторона ВС является гипотенузой этого треугольника , сторона DC катетом
в прямоугольном треугольнике гипотенуза всегда длиннее катетов , это значит ВС>CD
доказано
∠ABM = 30°;
Треугольники ABO и ABM подобны по двум углам. Поэтому
AO/AB = AM/BM; и AO/BO = AM/AB;
Из первого AO = AB*AM/9; из второго AO = AM/AB; (BO = 1);
Отсюда AB^2 = 9; AB = 3;
Площадь AOB = AB*BO*sin(30°)/2 = 3/4;
Площадь AOM в 8 раз больше, так как MO/BO = 8;
ответ 6.