Площадь прав тр через радиус вписанной окружности равен 3 корня из 3 на радиус в квадрате, а площадь вписанного круга равна Пи на радиус в квадрате.
Рассмотрим во сколько раз площадь треугольника больше площади круга. ![\frac{3 \sqrt[]{3}r^{2}}{\pi r^{2}}=\frac{3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/07e0a.png)
Пусть площадь круга х, тогда площадь треугольника (по условию) ![x+27\sqrt[]{3}-9\pi](/tpl/images/0144/4450/08b8d.png)
с одной стороны и ![\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/56410.png)
с другой.
Получим уравнение ![x+27\sqrt[]{3}-9\pi=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/99a9d.png)
Разрешим относительно х. Приведем к знаменателю Пи и приравняем числители
![\frac{x\pi}{\pi}+\frac{\pi27\sqrt[]{3}}{\pi}-\frac{9\pi^{2}}{\pi}=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/4f04e.png)
![x\pi}+\pi27\sqrt[]{3}-9\pi^{2}=x3 \sqrt[]{3}](/tpl/images/0144/4450/57c86.png)
Вынесем 3 корня из трех - Пи за скобки и получим
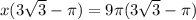
площадь круга = 9Пи
Найдем радиус круга
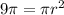
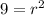
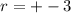
Т к радиус не может быть отрицательным то он равен 3
Площадь прав тр через радиус вписанной окружности равен 3 корня из 3 на радиус в квадрате, а площадь вписанного круга равна Пи на радиус в квадрате.
Рассмотрим во сколько раз площадь треугольника больше площади круга.
Пусть площадь круга х, тогда площадь треугольника (по условию) с одной стороны и с другой.
Получим уравнение
Разрешим относительно х. Приведем к знаменателю Пи и приравняем числители
Вынесем 3 корня из трех - Пи за скобки и получим
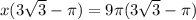
площадь круга = 9Пи
Найдем радиус круга
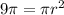
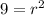
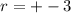
Т к радиус не может быть отрицательным то он равен 3
Объяснение:
1. Площадь трапеции вычисляется по формуле:
S=h*(a+b)/2 где h - высота трапеции, а - меньшее основание, в - большее основание. Все данные есть.
2. Чтобы найти периметр равнобокой трапеции нужно найти длину боковой стороны.
Высота трапеции проведенная к большему основанию из вершины, отсекает на нем отрезок равный (в-а)/2. Тогда в прямоугольном треугольнике, образованном высотой (катет), осеченным отрезком (второй катет) и боковой стороной (гипотенуза), по т. Пифагора боковая сторона - с=√(((в-а)/2)²+h²). Тогда периметр равнобокой трапеции равен:
Р=2√(((в-а)/2)²+h²) + а + в.
Все компоненты известны.