Восновании наклонной призмы лежит равнобедренный прямоугольный треугольник, катеты которого равны 7 см. боковая грань, проходящая через один из катетов основания, перпендикулярна плоскости основания, а площадь другой боковой грани, проходящей через катет основания, равна 56 см . найдите объем призмы, если ее боковые ребра наклонены к плоскости основания под углом 45 .

👇

Ответ:

Ибрагим002

28.05.2020

Дана наклонная призма АВСА₁В₁С₁.
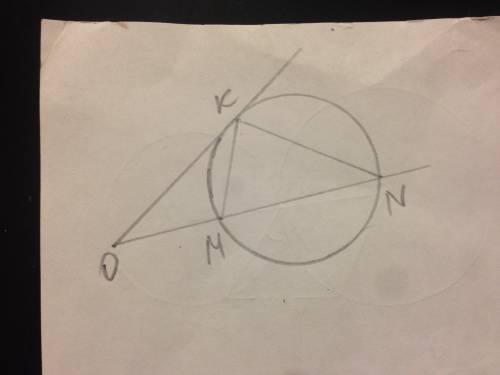
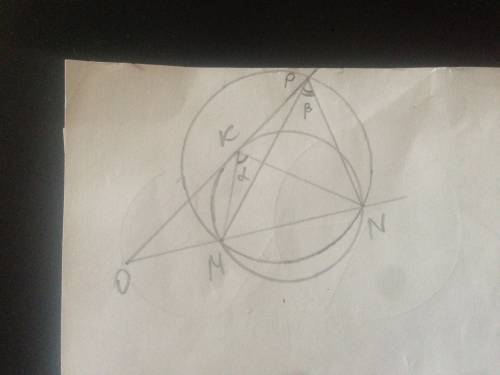
Треугольник АВС - прямоугольный равнобедренный, АВ=ВС=7.
Плоскость (АСС₁А₁) перпендикулярна плоскости АВС.

Проведём А₁К перпендикулярно АС, СМ параллельно А₁К,
СМ перпендикуляр к АС и ВС перпендикуляр к АС, значит угол МСВ- линейный угол двугоранного угла между плоскостями АСС₁А и АВС.
Угол МСВ=90⁰
,
АС перпендикуляр к ВС, АК- проекция АА₁ , по теореме о трех перпендикулярах АА₁ перпендикуляр к ВС.
Значит и СС₁ перпендикуляр в ВС. Четырехугольник ВВ₁С₁С- прямоугольник. Его площадь равна 56. Катет ВС=7, значит боковые ребра призмы 8
7*8=56
Из прямоугольного треугольника АА₁К зная угол А₁АК=45⁰ ( по условию) найдем высоту А₁К=4√2

V=S·H=1/2 АС·ВС·А₁К=1/2·7·7·4√2=98√2 кв ед.

Восновании наклонной призмы лежит равнобедренный прямоугольный треугольник, катеты которого равны 7

Восновании наклонной призмы лежит равнобедренный прямоугольный треугольник, катеты которого равны 7

4,5(53 оценок)

Открыть все ответы

Ответ:

margaRita2281

28.05.2020

S BB₁C₁C = ?

Работаем с 3-мя прямоугольниками. ABCD, ADC₁B₁, BCC₁B₁

Обозначим: АВ = CD = a, BC = AD = b, CC₁ = x

S BB₁C₁C = хb

SABCD = 12 = ab

SADC₁B₁ = 20 = b*DC₁ ( DC₁ ищем по т. Пифагора из ΔCDC₁

DC₁ = √(x² + a²)

20 = b*√(x² + a²)

рассмотрим систему уравнений:

20 = b*√(x² + a²)

12 = ab

Разделим 1-е уравнение на 2-е. Получим:

20/12 = √(x² + a²)/а, ⇒ 5/3 = √(x² + a²)/а | ², ⇒ 25/9 = (x² + a²)/а², ⇒

⇒25а² = 9(х² + а²), ⇒ 25а² = 9х² + 9а², ⇒16а² = 9х², ⇒ х² = 16а²/9, ⇒

⇒ х = 4а/3

Теперь смотрим S BB₁C₁C = хb = 4a/3*b = 4ab/3 = 4*12/3 = 16

ответ : S BB₁C₁C = 16см²

4,4(68 оценок)

Ответ:

Gay1122

28.05.2020

Точка К, из которой будет виден отрезок МN под наибольшим углом, будет находиться на общей окружности с точками М и N. При этом OK для неё является касательной.
По свойству касательной и секущей ОК²=ОМ·ОN.
Пусть ОМ=х, тогда ОN=OM+MN=x+6,
4²=x(х+6),
х²+6х-4=0,
х1=-8, отрицательное значение не подходит,
х2=2.
ON=2+6=8 дм - это ответ.

Теперь докажем, что отрезок MN виден из точки К под большим углом.
Пусть радиус окружности около тр-ка КMN равен r.
На стороне ОК в любом месте возьмём точку Р и опишем окружность около тр-ка РMN, радиусом R. ОР для неё является секущей, а для окружности, радиусом r - касательной, значит R>r.
Формула хорды: l=2R·sin(x/2), где х - градусная мера хорды.
∠MKN=α, ∠MPN=β.
Обратим внимание, что углы α и β - это половина градусной меры хорды.
MN=2R·sinβ ⇒ sinβ=MN/2R.
MN=2r·sinα ⇒ sinα=MN/2r.
Сравним синусы, предположив, что они равны.
MN/2R=MN/2r.
1/R=1/r, но R>r, значит 1/R<1/r, значит sinβ<sinα.
Так как градусная мера хорды не может быть больше 180°, значит в формуле хорды 0°<α<90°, 0°<β<90°.
В этом диапазоне синус угла тем больше, чем больше его градусная мера,
значит α>β.
Доказано.
Решить на одной из сторон острого угла с вершиной о отмечены точки м и n ( м лежит между о и n). на