1. Высота CD — это перпендикуляр, проведенный из вершины к противолежащей стороне. Значит ∠ВDС = ∠CDA = 90°.
Зная это, мы можем найти ∠ACD.
∠ACD = ∠CDA −∠CAD = 90° − 60° = 30° (согласно 1-му свойству прямоугольных треугольников: «сумма двух острых углов прямоугольного треугольника равна 90°»)
2. Теперь узнаем, чему равен угол BCD и угол DBC:
∠BCD = ∠ACB −∠ACD = 90° − 30° = 60°
∠DBC = ∠ВDС −∠BCD = 90° − 60° = 30°
3. Теперь, зная чему равны все углы треугольника, мы можем найти длину высоты CD, применяя 2-е свойство прямоугольных треугольников: «катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы»
Т.к. в треугольнике CBD катет BC лежит перед прямым углом CDB, теперь он будет являться гипотенузой этого треугольника.
Значит, CD = ¹/₂BC
CD = 5 ÷ 2 = 2,5.
ответ: ∠BCD = 60°; CD = 2,5 см.
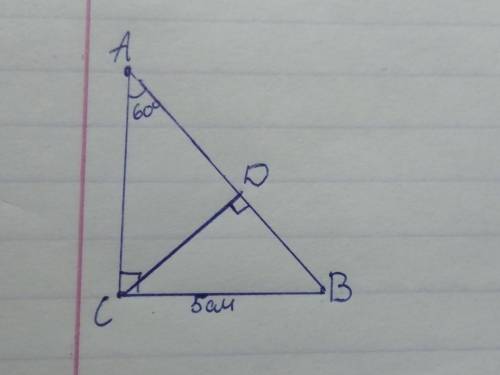
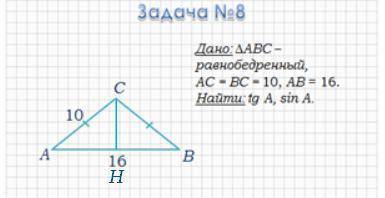
Задача: Дан ΔABC — равнобедренный, AC = BC = 10, AB = 16. Найти tg A, sin A.
Проведем высоту CH в ΔABC к стороне AB. Образуется два равных треугольника, т.к. ΔABC равнобедренный. AH = HB = 16/2 = 8.
Р-м ΔACH:
∠AHC = 90°, т.к CH — перпендикуляр к AH (AH∈AB) ⇒ ΔACH — прямоугольный.
Синус угла равен отношению противолежащего катета к гипотенузе.
Найдем катет CH за т. Пифагора:
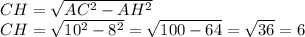
Тогда синус ∠A будет равен:
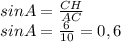
Тангенс угла равен отношению противолежащего катета к прилежащему:
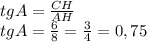
ответ: tg A = 0,75; sin A = 0,6.
tg α=AC/BC=2BC/BC=2
tg α=AD/PD, PD=AD/tg α=2/2=1
AP=√(AD²+PD²)=√4+1=√5
Треугольник KPD подобен треугольнику KBF с коэффициентом PD/BF=1/3 .
Поэтому PK/BK=1/3.
PK=KB-(AB-AP)=x-2x+√5=√5-x
(√5-x)/x=1/3
3(√5-x)=x
4x=3√5
x=3√5/4
AB=2x=3√5/2.
Треугольник APD подобен треугольнику ABC с коэффициентомAP/AB=√5*2/3√5=2/3
AD/AC=2/3, AC=3AD/2=3*2/2=3
PD/BC=2/3, BC=3PD/2=3*1/2=3/2=1.5