Вот пришло в голову решение :) Так-то задачка ерундовая :) Я продлеваю перпендикуляры HK и HM за точку H до пересечения с BA в точке A1 и BC в точке C1 (ну, точки лежат на продолжениях... из за того, что ∠ABC острый, эти точки есть и лежат где положено :) ) Для треугольника A1BC1 H - точка пересечения высот (ну двух-то точно :) - A1M и C1K), поэтому A1C1 перпендикулярно BH, и, следовательно, параллельно AC; то есть ∠BAC = ∠BA1C; Точки K и M лежат на окружности, построенной на A1C1, как на диаметре, поэтому ∠BA1C + ∠KMC = 180°; как противоположные углы вписанного четырехугольника. Или, что же самое, ∠BA1C = ∠BMK; следовательно ∠BAC = ∠BMK; и треугольники ABC и BMK имеют равные углы. То есть, подобны.
Следствие, которое важнее задачи :) Четырехугольник AKMC - вписанный. То есть через эти 4 точки можно провести окружность.
Дополнение. Тривиальный решения тут такой. ∠KHB = ∠A; ∠MHB = ∠C; BK = BH*sin(A) = BC*sin(C)*sin(A); BM = BH*sin(C) = BA*sin(A)*sin(C); То есть у треугольников ABC и MBK угол B общий, и стороны общего угла пропорциональны BM/BA = BK/BC = sin(A)*sin(B); значит треугольники подобны. коэффициент подобия sin(A)*sin(C), что тоже полезное следствие.
а)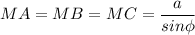
б)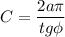
в)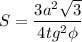
Объяснения:
Пусть К, Н и Р - середины сторон АВ, ВС и АС соответственно, тогда
АН⊥ВС, ВР⊥АС, СК⊥АВ (треугольник правильный, медианы, высоты и биссектрисы совпадают).
Центр О правильного треугольника АВС равноудален от вершин и от сторон треугольника, т.е.
АО = ВО = СО, КО = НО = РО, а эти отрезки - проекции соответствующих наклонных на плоскость треугольника, значит
МА = МВ = МС - расстояния от точки М до вершин
и МК = МН = МР - расстояния от точки М до сторон (МК⊥АВ, МН⊥ВС, МР⊥АС по теореме о трех перпендикулярах).
а) ΔМОС: ∠МОС = 90°,
___
____
Из прямоугольного треугольника МОК по теореме Пифагора:
___
____
б) СО - радиус описанной окружности. Тогда длина окружности:
_____
в)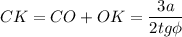
Площадь правильного треугольника АВС: