Объяснение: в треугольнике с 30,60,90 есть такое свойтво наименьший катет А(противолежит углу 30 ) а другой катет (протеволежит углу 60 )A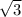
а гипотенуза равна 2A так вот в 4 задаче так и выходит СD=3,5 AD=7 и AC=3,5 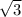тогда исходя из свойства угол D=60гр так как противолежит AC , так как СB=CD исходя из того что AC общая высота и для ACD и ABC то треугольник ABC равносторонний и угол В=60 5) тут аналогично используем тоже самое свойство уголs KPC=30 ; PKC=60 ;CKE=30;CEK=60 тогда СE=4,5 так как противолежит углу в 30гр и СK=4,5 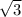; а PC=CK* = 
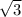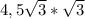=13,5 ответ CE=4,5 PC=13,5 если вам интересно откуда взялось это свойство то почитайте в интернете свойства треугольника с 30,60,90 градусами
Объяснение:
В данной работе я предлагаю вопросы для зачётов, задачи к этим зачётам и билеты к экзамену за курс геометрии 7 класса. Практический материал на экзамене можно предложить из задач к зачётам.
Надеюсь, что данная работа преподавателю математики проверить знания по данной дисциплине на начальной стадии её усвоения.
Для учащихся полезно будет по вопросам к зачётам готовить учебный материал самостоятельно, решая задачи, усваивать теоретические знания на практике, тем самым делая учебу интересной и успешной.
В 7 классе у наших детей появляется новый учебный предмет, который поначалу может показаться простым и не очень серьезным. Но это далеко не так. В былые годы наличие обязательного экзамена по геометрии с первых дней изучения новой дисциплины настраивало на серьёзный лад. Сейчас наличие задач по геометрии в ГИА и ЕГЭ по математике убедить учащихся в насущности и значимости предмета. Необходимость теоретических знаний понимается большинством учащихся при решении задач, доказательстве теорем, везде, где не обойтись без аргументированных объяснений. Задача учителя не только донести знания по предмету, но и заставить овладеть ими. Готовясь к зачётам дети вынуждены самостоятельно разбирать, заучивать учебный материал, а также консультироваться у учителя, друг у друга, доказывая друзьям теоремы и решая задачи на дополнительных занятиях и консультациях по математике. Этот процесс – объяснение товарищу – очень нравится ребятам, они при этом повышают свою самооценку, мотивацию к учебе, повышают качество собственных знаний. Учащиеся сначала побаиваются зачетов, но в процессе подготовки и при проведении понимают их необходимость, поэтому относятся более ответственно к данной технологии. Но как любое полезное для детей мероприятие, подготовка зачёта и экзамена, требует серьёзной и кропотливой работы со стороны взрослых, в данном случае – учителя математики. Надеюсь своей работой облегчить на начальном этапе труд педагога при подготовке к зачету по геометрии в 7 классе.
Для решения данной задачи нужны в основнои рассуждения.
В равнобокой трапеции диагонали равны и каждая составляет с основанием одинаковый угол.
Из вершины С проведем параллельно диагонали BD прямую до пересечения с продолжением АD.
Обозначим точку пересечения Е.
Четырехугольник ВСЕD - параллелограмм, т.к. противоположные стороны параллельны, и СЕ равно BD .
Следовательно, DE=ВС, и
АЕ - равна сумме оснований.
Площадь трапеции АВСD равна половине произведения ее высоты СМ на АЕ - сумму оснований.
Площадь равнобедренного треугольника АСЕ равна половине произведения его высоты на АЕ.
Высота трапеции и треугольника общая.
Площади данной трапеции и площадь получившегося треугольника равны. Опустим из С высоту СМ и отложим на её продолжении отрезок МР, равный СМ.
Соединив А и Р, получим равнобедренный треугольник АСР , т.к. треугольники АСМ и АМР равны по двум сторонам и прямому углу при М между ними.
В треугольнике АСР угол при вершине А равен 30 градусам ( 15+15).
Из С опустим на сторону АР высоту СН.
Её длина, как длина катета, противолежащего углу 30 градусов, равна половине АС и равна α/2
S Δ АСР равна АР*СН:2=α·α/4=α²/4
Треугольник АСР равен треугольника СМЕ, и площадь треугольника АСР равна площади треугольнка АСЕ, т.е. равна площади трапеции.
ответ: Площадь трапеции равна α²/4