В прямоугольный ΔАВС, ∠С=90 вписан круг .Биссектриса ∠А делит катет в отношении CD:DB=3:5. Найдите площадь круга
Решение Площадь круга S= πr² .Радиус вписанной окружности найдем из формулы S=1/2*P*r .
1) Тк " биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника" , то CD:СА=ВD:АВ или 3:СА=5:АВ ⇒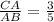
, а это по определению sinB .
2) По основному тригонометрическому тождеству
sin²B+cos²B=1 получаем cosB=√(1-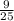
)=
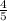
3) cosB=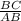 
или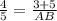 
⇒ AB=10.
По т Пифагора АС=√(АВ²-ВС²)=√(100-64)=6
4) S=1/2*P*r
1/2*BC*AC=1/2*(AB+BC+AC)*r
1/2*8*6=1/2*24*r ⇒ r=2 ед
S(круга)=π*2²=4π (ед²)
1) Если все боковые стороны (это рёбра) пирамиды имеют одинаковую длину, то их проекции на основание - радиусы R описанной окружности вокруг основания.
Радиус равен половине диагонали основания.
R = √(3² + 4²) = 5 см.
Тогда высота Н пирамиды равна:
Н = √(13² - 5²) = √(169 - 25) = 12 см.
2) Будем считать, что в задании имеется в виду, что высота пирамиды проецируется на основание в вершину прямого угла.
Тогда 2 боковых грани пирамиды вертикальны, одна - наклонная.
Гипотенуза основания равна √(9² + 12²) = 15 см.
Высота основания на гипотенузу равна (9*12)/15 = (36/5) = 7,2 см.
Высота наклонной боковой грани равна √(8² + 7,2²) = 0,8√181 ≈ 10,7629 см.
Теперь можно определить площади боковых граней.
Sбок = (1/2) *(6*8 + 12*8 + 15*(4/5)√181) = (72 + 6√181) см².
Площадь основания Sо = (1/2)(9*12) = 54 см².
Полная площади пирамиды равна 54 + 72 + 6√181 = 126 + 6√181 см².
Объём пирамиды равен (1/3)*54*8 = 144 см³.
16х^+9x^2=400
25x^2=400
x^2=16
x=4
3х=12 4х=16
S=12*16=192
P=(12+16)*2=56