Дано:
P-12 см
Сторона -5см
Найти:
Основание-?
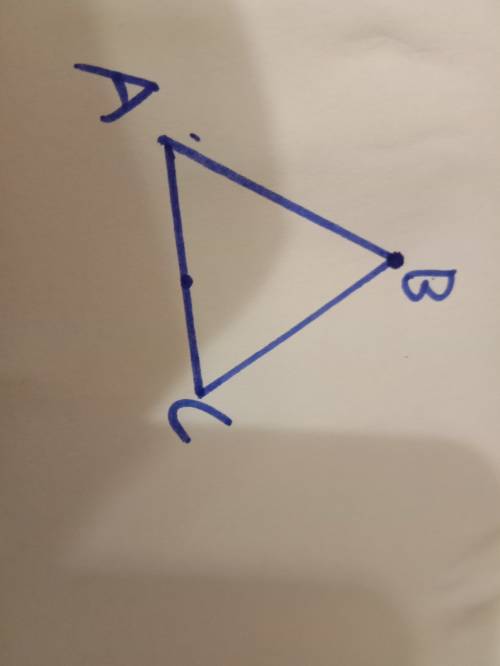
Периметр -это сумма длин всех сторон треугольника. Допустим, что у нас треугольник ABC. (смотри картинку) Так как у треугольника Два основания одинаковы, значит, что вторая сторона тоже будет равна 5 см. Чтобы найти боковую сторону надо сложить два основания и из периметра вычесть сумму основания. Вот действия:
1) 5+5=10 (см) - две основные стороны
2) 12-10=2 (см) -это боковая сторона.
ответ: боковая сторона =2 см.
Чтобы лучше запомнил(а) я напишу, как найти боковую сторону у треугольника ABC.
AB и BC - основания.
AC-боковая.
Так как AB =5см , то и BC =5 см.
Периметр - 12 см. Нужно найти AC.
1) AB+BC=5+5=10 (см)- основание AB и BC.
2) P-(AB+BC)=12-10=2 (см) - боковая сторона- AC.
ответ: боковая сторона AC =2 см.
Надеюсь
В равностороннем треугольнике все углы равны 60°.
Высоты, по свойству высоты равнобедренного треугольника, являются биссектрисами и медианами, и каждая делит его на 2 равных прямоугольных треугольника.
Высота в таких треугольниках является большим катетом, который противолежит углу 60°, сторона равностороннего треугольника- гипотенузой, а меньший катет противолежит углу 30° и равен половине гипотенузы (свойство)
-----------------
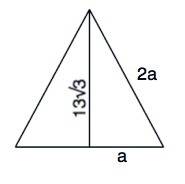
Примем меньший катет (половину стороны) равным а. Тогда гипотенуза (сторона равностороннего треугольника) равна 2а.
По т.Пифагора с²=a²+b² (с- гипотенуза, а и b- катеты)⇒
(2а)²=а²+((13√3)²⇒
3а²=13²•3 ⇒ а=13,
Сторона данного равностороннего треугольника 2а=26 (ед. длины)
или
с=b:sin60°, где с - сторона равностороннего треугольника, b- его высота.
с=(13√3):(√3/2)=26 (ед. длины)
О2N = √(O2B²-NB²) =√(100-36)=8.
В прямоугольном треугольнике РNМ: РМ = R2+R1 = 10+x (так как О2PMO1 - параллелограмм), PN= O2N-O2P = 8-x (так как в параллелограмме О2PMO1 O2P=O1M), NM = NB+BM=6+6=12. Тогда по Пифагору МР²=NP²+NM² или (10+х)²=(8-x)²+144, или 100+20х+х²=64-16х+х²+144, откуда х=3.
ответ: радиус первой окружности равен 3.