№1. Т.к. угол BAD= углу BCM, а BC параллельно AD, то ABCM - параллелограмм. Тогда AB=CM=2, BC=AM=3.
№2 Т.к. нам даны углы в 90 градусов, то данная нам трапеция прямоугольная. Опустим высоту СМ из точки С. Тогда АВСМ - прямоугольник. СМ=АВ=8, ВС=АМ=4. По теореме Пифагора найдем CD из треугольника CMD, получаем MD=6. Значит AD=10. Площать ACD= половине высоты на сторону, к которой проведена высота, значит площадь ACD равна 40. А площать трапеции равна половине суммы оснований и умножить на высоту, площадь трапеции равна 56.
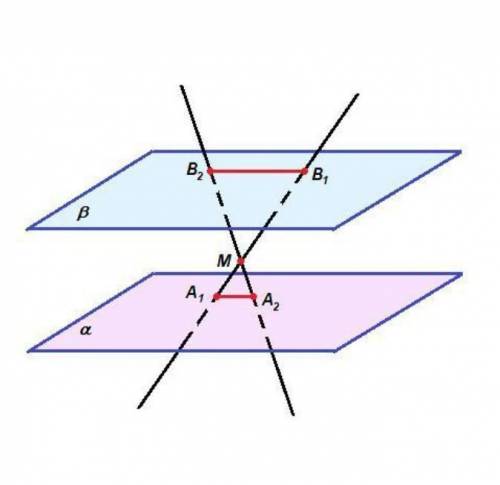
Пересекающиеся прямые А₁В₁ и А₂В₂ задают плоскость, которая пересекает плоскости α и β по прямым А₁А₂ и В₁В₂, значит
А₁А₂ ║ В₁В₂.
Тогда ∠МВ₁В₂ = ∠МА₁А₂ как накрест лежащие при пересечении параллельных прямых А₁А₂ и В₁В₂ секущей А₁В₁,
∠В₁МВ₂ = ∠А₁МА₂ как вертикальные, значит
ΔВ₁МВ₂ подобен ΔА₁МА₂ по двум углам.
МВ₂ = А₂В₂ - МА₂ = 10 - 4 = 6 см
\dfrac{A_{1}A_{2}}{B_{1}B_{2}}=\dfrac{MA_{2}}{MB_{2}}
B
1
B
2
A
1
A2
=
MB
2
MA
2
Пусть А₁А₂ = х, тогда В₁В₂ = х + 1,
\dfrac{x}{x+1}=\dfrac{4}{6}
x+1
x
=
6
4
6x = 4(x + 1)
6x = 4x + 4
2x = 4
x = 2
А₁А₂ = 2 см