Вписать в окружность можно только равнобедренную трапецию.
Диагонали равнобедренной трапеции равны, при пересечении образуют с её основаниями равнобедренные треугольники.
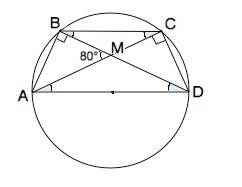
В трапеции АВСD ∆ АМD равнобедренный, его внешний угол при вершине М=80° и равен сумме двух не смежных с ним (свойство внешнего угла).
Углы при основании равнобедренного треугольника равны. =>
угол МАD=углу MDA=80°:2=40°
АD- диаметр, поэтому по свойству вписанного угла ∠АСD=90°
∠АСВ=∠DВC=40° – как накрестлежащие равным углам при АD.
∠АВС=∠ВСD=90°+40°=130°
Cумма углов, прилежащих к боковой стороне трапеции, равна180° =>
угол АDC=180°-130°=50°
ответ: ∠А=∠D=50°, ∠В=∠С=130°.
рассмотрим четырехугольник ABCD. угол А-90 по условию. СH-высота. значит угол H-90. угол B-тоже 90 т.к. трапеция прямоугольная. зн. угол BCH - тоже 90(360-(90+90+90)=90). зн. этот четырехугольник - прямоугольник т.к. у прямоугольника все углы по 90. BC параллельна AD и секущей AC. угол АCH- 45(как накрестлежащий при вышесказанных параллельных). рассмотрим треугольник ACD. угол САН - 45(т.к. угол А -90 а угол САВ - 45. зн. 90-45=45) угол D=45. по вычислению(360 - (90+90+135). зн. этогт треугольник равнобедренный. а в равнобедренном треуг. биссекктриса - медиана и высота. зн. АН=НD=15.Теперь рассмотрим треуг АВС и треуг. АНС. они равны по катету и гипотенузе(гипотенуза - общая а в прямоугольнике противоположные стороны равны. тоесть АН=ВС=15). значит этот четырехугольник - квадрат. значит все стороны равны значит наименьшая боковая сторона равна 15. вроде так)))