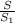 =
= 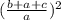 =
= 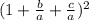 (1)
(1)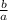 =
= 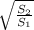 (2)
(2)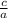 =
= 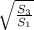 (3)
(3)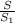 =
= 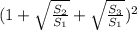 =
= 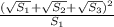
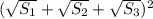
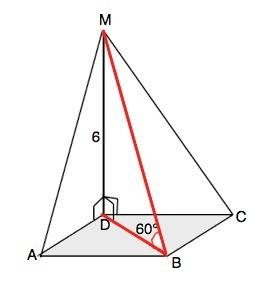
а) По условию MD перпендикулярна плоскости квадрата,
АD -проекция АМ на плоскость квадрата.
СD - проекция СМ на плоскость квадрата.
По т. о 3-х перпендикулярах МА⊥АВ, и МС⊥СВ.
Углы МАВ и МСВ прямые,⇒ ∆ МАВ и Δ МСВ прямоугольные.
б) В прямоугольном ∆ МDB катет DB равен MD:tg60°=6:√3=2√3
BD- гипотенуза прямоугольного равнобедренного ∆ ABD, его острые углы=45°.
АВ=ВD•sin45°=2√3•√2/2=√6
в) МD перпендикулярна плоскости квадрата по условию.
В ∆ АВD катет АD является проекцией наклонной АМ на плоскость квадрата.
Гипотенуза DB является проекцией МВ на плоскость квадрата.
АВ - общий катет ∆ АМВ и ΔΔ ADB. ⇒ ∆ ABD является проекцией ∆ MAB на плоскость квадрата.
в) В ∆ МАВ по т. о 3-х перпендикулярах наклонная МА⊥АВ,⇒
∆ МАВ прямоугольный.
Ѕ=AM•AB:2
Из ∆ АМD по т.Пифагора АМ=√(MD²²+AD²²)=√(36+6)=√42
S=√42•√6=√(7•6•6)=6√7 см²
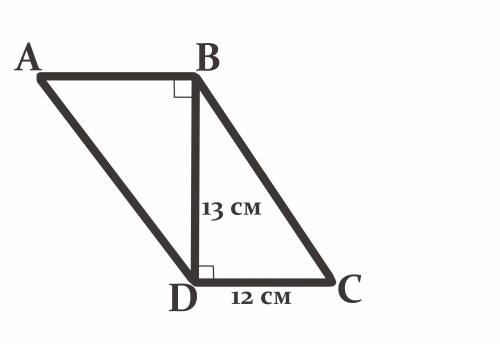
Дано :
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
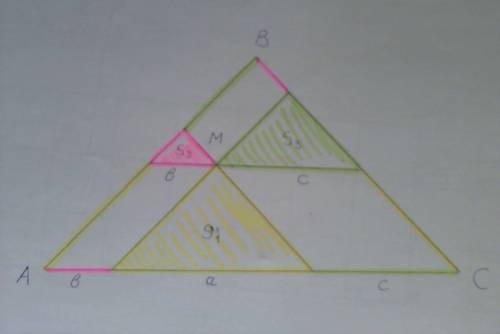
а параллелограммы на вертикальных углах I, II, III соответственно.
пусть при вершине М - углы в W1 и I = альфа; W2 и II = бета; W3 и III = гамма
Пусть вершины треугольника W1 буду MEF, W2 MGH, W3 MPQ
Заметим, что треугольники W1, W2, W3 подобны, тк все три угла у них равны
Запишем площади W1, W2, W3, I,II,III
S1 =
S2 =
S3 =
I =
II =
III=
Запишем отношения
I/S1 =
Аналогично
II/S2 =
III/S3 =
то есть: I = S1*
II = S2*
III = S3*
S(ABC) = S1+S2+S3+I+II+III обозначим это равенство (!)
Из подобия треугольников W1, W2, W3 получаем:
А теперь если подставить все это счастье в равенство (!), получим
S(ABC) =
то есть