Длины параллельных сторон трапеции равны 4 и 25 см , а длины боковых сторон - 20 см и 13 см . найдите - id284085820220618 от sasd2 18.06.2022 19:36

Question

Геометрия: Длины параллельных сторон трапеции равны 4 и 25 см , а длины боковых сторон - 20 см и 13 см . найдите высоту трапеции

sasd2 · Accepted Answer

Для любой правильной призмы справедливы формулы:

Площадь боковой поверхности:

Sбок = Pосн · h, где

Росн - периметр основания,

h - высота.

Площадь полной поверхности:

Sполн = Sбок + 2Sосн

Объем:

V = Sосн · h

____________________

a - сторона основания.

____________________

Правильная треугольная призма:

в основании лежит правильный треугольник, значит

Sосн = 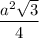$\dfrac{a^{2}\sqrt{3}}{4}$

Sбок = 3а · h

Sполн = 3a · h + 2 · a²√3/4 = 3ah + a²√3/2

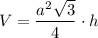
$V=\dfrac{a^{2}\sqrt{3}}{4}\cdot h$

____________________

Правильная четырехугольная призма:

в основании - квадрат, значит

Sосн = a²

Sбок = 4ah

Sполн = 4ah + 2a²

V = a²h

____________________

Правильная шестиугольная призма:

Sосн = 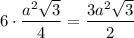$6\cdot \dfrac{a^{2}\sqrt{3}}{4}=\dfrac{3a^{2}\sqrt{3}}{2}$

Sбок = 6ah

Sполн = 6ah + 2 · 3a²√3/2 = 6ah + 3a²√3

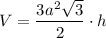
$V=\dfrac{3a^{2}\sqrt{3}}{2}\cdot h$

Длины параллельных сторон трапеции равны 4 и 25 см , а длины боковых сторон - 20 см и 13 см . найдите высоту трапеции