В трапеции АВСD углы, прилежащие к боковой стороне, в сумме равны 180° (как односторонние при параллельных прямых ВС и АD и секущих - боковых сторонах АВ и СD). =>
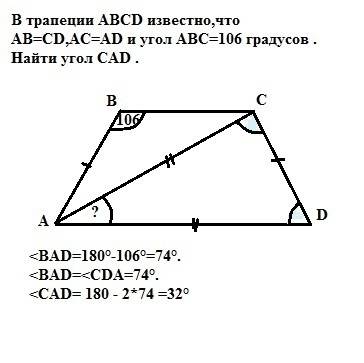
<BAD = 180° - 106° = 74°.
Так как АВ=СD - трапеция равнобедренная, то углы при основаниях равны => <BAD=<CDA = 74°.
Так как AC=AD (дано) => треугольник DAC равнобедренный и углы при основании CD равны. <ACD=<CDA = 74°.
Тогда угол при вершине треугольника САD равен 180-2*74= 32° (так как сумма внутренних углов треугольника равна 180°)
ответ: угол САD=32°.
Можно также рассмотреть треугольник ABC с длиной стороны AC стремящейся к нулю. Не трудно показать, что в этом случае описанная в условии окружность должна касаться линии AB вблизи стремящейся к нулю окрестности точки B, длина AB будет равна 10/2 = 5, а угол между AB и направлением на центр искомой окружности равен 60 (половине 120 - центр будет лежать на биссектрисе к углу A). То есть имеем прямоугольный треугольник ABO (угол B - прямой) с углом A = 60 градусов и катетом AB = 5. AO = 5/sin(60) = 10.