Пусть одна сторона квадрата АВСD будет х. Тогда периметр будет равен: 4*х=8, отсюда, х = 2. Пусть КD = y, на рисунке отмечено, что у равны также и AP, BM, CN. Между собой равны и ND, MC, BP, AK. Это следует из того, что нам дан квадрат. Теперь ND/KD=tg30=1/√3. Отсюда ND=KD/√3. А KD+ND=2. Решаем систему из этих 2-х уравнений:
ND*√3+ND=2
ND=2/(√3+1)=2*(√3-1)/(3-1)=√3-1.
Так как сторона ND лежит против угла в 30 градусов, она равна половине гипотенузы. Значит KN=ND*2=2(√3-1). Все маленькие треугольники равны друг другу по двум сторонам и углу между ними. Значит нам фигура внутри - квадрат. И его периметр: 4*2(√3-1)=8(√3-1)
Дается один из возможных вариантов решения. ( На сайте есть и другой).
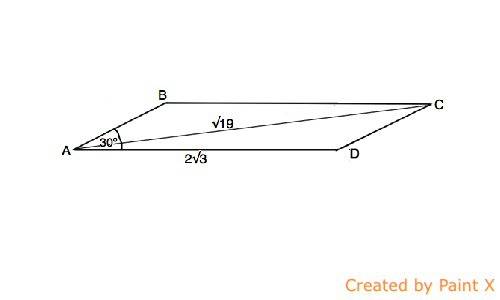
Пусть параллелограмм будет АВСD,
сторона АD=2√3, диагональ АС=√19, ∠ ВАD=30°
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180° ( из свойства углов при параллельных прямых и секущей).
Тогда ∠ АDС=150°
По т.косинусов из ∆ АDС:
АС²=АD² +СD² - 2•AD•CD•cos ∠ADC
Примем СД=х
cos150ª= -cos30º= -(√3):2
19=12+х²-2•2√3•(-√3):2 ⇒
х²+6х-7=0⇒
D=b²-4ac=6²-4•-7=64
x₁=-(6)+√64):2=1;
х₂= -(6)-√64):2=-7 ( не подходит)
Противоположные стороны параллелограмма равны. АВ=CD
Меньшая сторона параллелограмма равна 1 см.
АВ²=ВС²+АС²-2*ВС*АС*cosC
AB²=8²+5²-2*8*5*cos30
AB²=64+25-80*√3/2
AB²=89-40√3