8) Рас. треугольник ВСД
Угол ДВС равен 40°, т.к. он и внешний угол В вертикальны. Т.к. в треугольнике DВС один угол 90°, а другой 40°, то угол ВСD равен 50°
Рас. треугольник АВD
Угол А смежный с углом 2, т.е. равен 180-110=70°
Т.к. треугольник прямоугольный, то угол АВD равен 90-70=20°
Значит, угол АВС равен 20+40=60°
Угод ВАD 70° и угол ВСD 50° по решенному
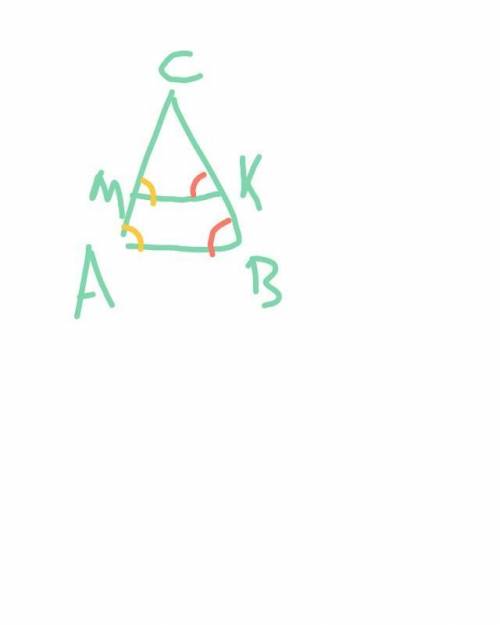
9) Смотри по рисунку
Желтым и красным обозначены пары равных углов, равны они как соответственные, при АВ||МК и секущих АС и ВС
И т.к. угол А равен углу В (АВС - равнобедренный, значит углы при основании равны), то и углы М и К равны
Треугольник МСК равнобедренный по определению равнобедренного треугольника
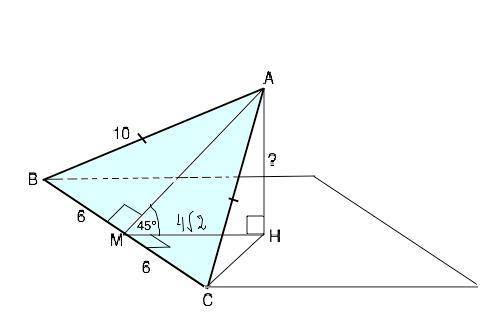
ответ:4√2 см.
Требуется найти расстояние от вершины А до плоскости, следовательно, основание ВС лежит в проведенной плоскости, с которой плоскость треугольника ВАС образует двугранный угол с ребром ВС. Сделаем и рассмотрим рисунок.
Расстояние от точки до плоскости равно длине опущенного на нее из точки перпендикуляра ⇒ АН - искомое расстояние.
Проведём НМ⊥ВС. По т. о 3-х перпендикулярах наклонная АМ⊥ВС. Отрезки АМ и МН образуют угол 45°. АМ⊥ВС ⇒ АМ является высотой и медианой равнобедренного ∆ ВАС. ∆ ВАМ - египетский, т.к. ВМ:АМ:АВ=3:4:5, ⇒ АМ=8 см ( можно проверить по т.Пифагора). Тогда АН=АМ•sin45°=8•√2/2=4√2 см
Объем=Площадь основы*высота
1. Найдем площадь основы
Полная поверхность (ПП)=Боковая Поверхность (БП)+Площадь основы (ПО)
БП=ПО*высота
ПП=(ПО*высота)+ПО=ПО*(высота+1)
ПО=ПП/(высота+1)
ПО=168п/(8+1)=18,5п (см"2)
2. Найдем объем
Объем=ПО*выота
Объем=18,5п*8=148п(см"2)
ответ: 148 см"2 - объем цилиндра