Sc = d²·tgα·√2/(2+tgα).
Sб = 4d²·tgα/(2+tgα).
So = d²/(2+tgα).
So =
Объяснение:
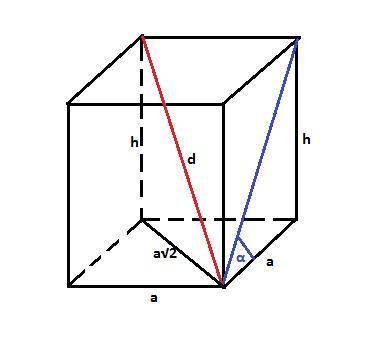
Призма правильная, значит в основании лежит квадрат. Пусть сторона квадрата равна "а". Тогда диагональ квадрата равна а√2.
Высота призмы равна h = a·tgα (из прямоугольного треугольника - половины боковой грани).
Квадрат диагонали призмы d² = h²+2a². (из прямоугольного треугольника - половины диагонального сечения).
d² = a²·tg²α+2a² = a²(2+tgα). => a = d/(√((2+tgα)).
h = a·tgα = d·tgα/(√((2+tgα)).
Тогда площадь диагонального сечения равна:
Sc = a√2·h = d√2/(√(2+tgα))·dtgα/(√(2+tgα)) = d²·tgα·√2/(2+tgα).
Площадь боковой поверхности равна произведению периметра основания на высоту призмы:
Sб = 4·a·h = 4d/(√((2+tgα))·d·tgα/(√((2+tgα)) = 4d²·tgα/(2+tgα).
Площадь основания (квадрата) равна квадрату стороны:
So = a² = d²/(2+tgα).
Кроме того, в равностороннем треугольнике биссектриса является также медианой и высотой. Известно, что отношение высоты равностороннего треугольника к его стороне равно √3/2. Значит, сторона треугольника равна 11√3*(2/√3)=22. Площадь треугольника равна половине произведения основания на высоту, то есть, 1/2*22*11√3=121√3.