Назовем высоты треугольника ВН, АН1, СН2.
1. Найдем угол АОН=180-угол АОВ=180-110=70, тогда угол ОАН=180-угол АОН-угол ОНА=180-70-90=20. Угол СОН=180-угол ВОС=180-110=70, тогда угол ОСН=180-угол СОН-угол ОСН=180-70-90=20
2. Угол Н2ОА=180-угол АОН-угол СОН=180-70-70=40, тогда угол Н2АО=180- угол ОН2А-угол Н2ОА=180-90-40=50. Угол СОН1=180-угол НОС-угол АОН=180-70-70=40. Угол ОСН1=180-угол ОН1С-угол СОН1=180-90-40=50.
3. Угол А=угол Н2АО+угол ОАН=50+20=70. Угол С=угол ОСН1+уголОСН=50+20=70. Отсюда угол А=углу С=70 треугольник АВС-равнобедренный углы при основании АС равны по 70 градусов, боковые стороны АС и ВС.
Угол В=180-угол А - угол С=180-70-70=40
Найдем, как связаны радиусы вписанных окружностей.
Пусть сторона правильного треугольника равна a.
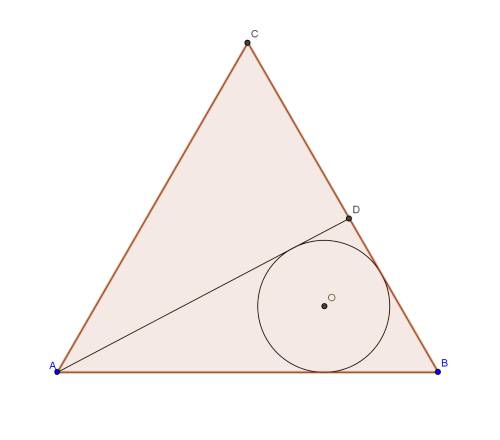
Сначала нужно найти длину отрезка AD. Проще всего это сделать по теореме косинусов.
Посмотрим на треугольник ABD. В нем BD = 7/15 a, AB = a, угол B = 60 градусов.
Тогда 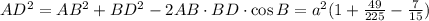 ,
,
AD = 13/15 a
Периметр треугольника ACD = a + 8/15 a + 13/15 a = 36/15 a, треугольника ABD = a + 7/15 a + 13/15 a = 35/15 a.
С одной стороны, площадь треугольника - половина прооизведения высоты на сторону, с другой - половина произведения периметра на радиус списанной окружности. Если считать по первой формуле, получим, что S1/S2 = CD/DB = 8/7 (здесь индекс 1 соответствует треугольнику ACD). По второй: S1/S2 = (36*r1)/(35*r2).
Итак, 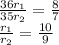
Площади кругов пропорциональны квадратам радиусов, поэтому площади относятся как 100 к 81.
Есдиственный вопрос, площадь какого из кругов дана. Отсюда и 2 ответа: 81*100/81=100 или 81*81/100=65.61
ответ: 100 или 65,61.
Четырёхугольная пирамида-правильная, следовательно в её основании лежит правильный четырёхугольник-квадрат.
Периметр квадрата равен 1 м, значит его сторона равна 1:4=1/4 м.
Площадь боковой поверхности представляет собой 4 площади треугольника с основанием 1/4 м и высотой 1/4 м (апофема).
Sбок=4*(1/2 * 1/4*1/4)=4*1/32=1/8=0,125 (м2)