Дана равнобедренная трапеция. известна сторона bc=15, ad=49см, также дан уголd=60 градусов. необходимо найти периметр трапеции.

👇

Ответ:

12345678йцуке

15.04.2023

Дано: равнобедренная трапеция АВСD. АВ=СD
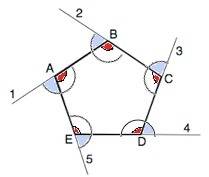
Меньшее основание ВС=15 см
большее основание AD=49 см
острые углы D=A=60 град.
Найти: Р=?
Решение: Опустим перпендикуляры к большему основанию СN и ВM. МN=BC=15 cм, АМ=АN=(49-15):2=17 см
Рассмотрим треугольник АВМ. Угол А=60, следовательно угол В=30, т.к. сумма острых углов прямоугольного треугольника=90 град.
Катет лежащий против угла в 30 град.= половине гипотенузы, значит АВ=2*13=34.
Теперь известны все стороны трапеции АВ=СD=34, ВС=15, АD=49
Р=34*2+15+49=132 см
ответ: периметр трапеции равен 132 см.

4,4(58 оценок)

Открыть все ответы

Ответ:

Мур3иk

15.04.2023

1. Задача 1. решена пользователем
ХироХамаки Новичок
(решение в файле)

2. Условие задачи 2. неточное. Должно быть:
Основание АС равнобедренного треугольника лежит в плоскости α. Найдите расстояние от точки В до плоскости α, если АВ = 5, АС = 6, а двугранный угол между плоскостью треугольника и плоскостью α равен 60 градусам.

Проведем ВН⊥АС и ВО⊥α.
ВО - искомое расстояние.
ОН - проекция ВН на плоскость α, значит ОН⊥АС по теореме, обратной теореме о трех перпендикулярах.
∠ВНО = 60° - линейный угол двугранного угла между плоскостью α и плоскостью треугольника.
АН = НС = 6/2 = 3 (ВН - высота и медиана равнобедренного треугольника)
ΔАВН: по теореме Пифагора
ВН = √(АВ² - АН²) = √(25 - 9) = √16 = 4
ΔВНО: ВО = ВН · sin 60° = 4 · √3/2 = 2√3

3. АО⊥α, ОВ и ОС - проекции наклонных АВ и АС на плоскость α, тогда
∠АВО = ∠АСО = 60°.
ΔАВО = ΔАСО по катету и противолежащему острому углу (АО - общий катет и ∠АВО = ∠АСО = 60°), значит
АВ = АС = 6.

Много сделайте хоть что нибудь, желательно с чертежом 1) отрезок кс – перпендикуляр к плоскости треу

Много сделайте хоть что нибудь, желательно с чертежом 1) отрезок кс – перпендикуляр к плоскости треу

4,8(1 оценок)

Ответ:

nastusya0307

15.04.2023

Углы, смежные с внутренними углами многоугольника, называются внешними.

Сумма внешнего и внутреннего угла при одной вершине равна градусной мере развернутого угла =180°

Сумма внешних углов многоугольника равна разности между суммой всех таких развернутых углов и суммой внутренних углов многоугольника.

Как известно, сумма внутренних углов многоугольника находится по формуле N=180°•(n-2)

Поэтому сумма внешних углов

180°•n-180•(n-2)=180°•n-180°•n+360°=360°

Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна 360°.
Докажите,что сумма внешних углов выпуклого многоугольника равна 360 градусов