Прямой угол меньше тупого угла. Поэтому высота тупоугольного треугольника, проведенная из вершины острого угла, всегда расположена вне самого треугольника и пересекает не саму сторону, к которой проведена, а её продолжение. Об этом важно помнить.
В равнобедренном треугольнике АВС углы при основании АС равны по (180°- ∠АВС):2=(180°-112°):2=34°
АF- биссектриса. Поэтому ∠FAC=∠BAF= ∠ BAC:2=34°:2=17°
Из суммы углов треугольника
∠BFA=180°-∠BAF-∠ABF=180°-17°-112°=51°
Сумма острых углов прямоугольного треугольника 90° ⇒
∠НАF=90°-51°=39°
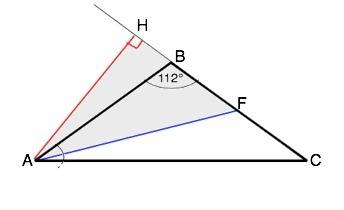
Углы при основании равны, то есть если основание АС, то угол А = углу С.
Так как сумма углов любого треугольника равна 180 гр, то сумма углов А+С = 180-112=68 гр. Угол А=углу С = 68:2=34 гр.
Так как АF- биссектриса, то угол ВАF= углу САF= 34:2=17 гр.
Рассмотрим треуг. АВF, угол В=112 гр, угол ВАF=17 гр., тогда угол ВFА= 180 -112-17=51 гр.
Рассмотрим треуг АНF, угол АНF=90 гр, угол АFН=51 гр, тогда по свойству прямоугольного треугольника НАF= 90-51= 39 гр.
ответ F=51 гр, А=39 гр, Н=90 гр.
tg α = sin α \ cos α = √5\3 : (-2\3) = -√5\2
ctg α = 1 \ tg α = 1 \ (-√5\2) = -2\ √5 = -2√5 \ 5
2. cos α = √(1-sin²α) = √(1-1\16) = √(15\16) = √15\ 4
tg α = 1\4 : √15\4 = 1\√15 = √15\ 15
ctg α = 1 \ 1\√15 = √15