По заданным величинам находим углы треугольника.
C = arc sin(20/25) = arc sin(4/5) = 53,1301 градуса .
B = arc cos (7/25) = 73,7398 градуса.
Угол А = 180 - В - С = 53,1301 градуса .
Значит, треугольник - равнобедренный: АВ = ВС = 25.
Тогда АС = 2√(25² - 20²) = 2√(625 - 400) = 30.
Находим ДН из условия подобия треугольников НДС и АВД и равенства взаимно перпендикулярных углов НСД и АВД.
ДН/ДС - АД/ВД. Здесь точка Н - точка пересечения высот.
ДН = 15*15/20 = 11,25.
Используя формулу деления высот точкой их пересечения
ВН/НД = cos B/(cos A*cosC), находим отрезки.
Отрезки на сторонах. отсекаемые высотами
АС₂ = 18 С₂B = 7 AB = 25 25
BA₂ = 7 A₂C = 18 BC = 25 25
АB₂ = #ДЕЛ/0! B₂C = #ДЕЛ/0! AC = #ДЕЛ/0! 30
Точка В2 это точка Д, она делит АС пополам,АД = 30/2 = 15.
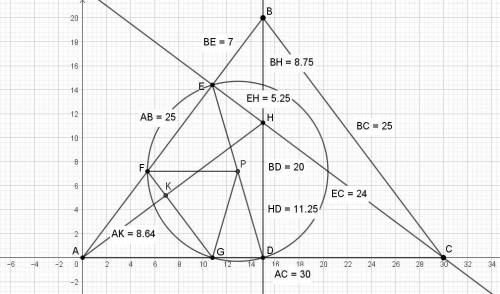
Далее удобнее решать в прямоугольной системе координат,
Пусть А(0; 0), В(15; 20), С(30; 0).
Находим координаты точки Е из подобия АЕ к АВ = 18/25.
х(В) = 15*(18/25) = 54/5 = 10,8.
у(В) = 20*(18/25) = 72/5 = 14,4. Точка E(10,8; 14,4), точка Д(15; 0).
Находим координаты центра Р окружности на ДЕ.
Р = (10,8+15)/2; (14,4+0)/2) = (12,9; 7,2).
Радиус окружности равен РЕ = √(15-12,9)² + (0-7,2)²) = 7,5.
Уравнение окружности (x-12,9)² + (y-7,2)² = 7,5².
Уравнение прямой АВ по угловому коэффициенту: у = (20/15)х или у = (4/3)х.
Находим координаты точки F как точки пересечения АВ с окружностью, решая систему:
{ у = (4/3)х.
{ (x-12,9)² + (y-7,2)² = 7,5². После подстановки у= (4/3)х во второе уравнение находим х = 27/5 = 5,4, а у = 36/5 = 7,2.
Второй корень повторяет координаты точки Е(10,8; 14,4).
Координаты точки G находим аналогично, толь как точку пересечения с осью Ох в виде уравнения у = 0.
G(10.8; 0). Второй корень повторяет координаты точки D(15; 0).
Уравнение прямой АН: у = (11,25/15)х.
Уравнение GF. Вектор GF = (5,4; -7,2).
Уравнение GF:( (x - 10,8)/5,4) = y/(-7,2).
Координаты точки К находим как точку пересечения прямых АН и GF, решая систему:
{ у = (11,25/15)х.
{ ( (x - 10,8)/5,4) = y/(-7,2).
Решение даёт значение х(К) = 6,912, у(К) = 5,184.
Длина АК = √(6,912² + 5,184²) = 8,64.
ответ: АК = 8,64.
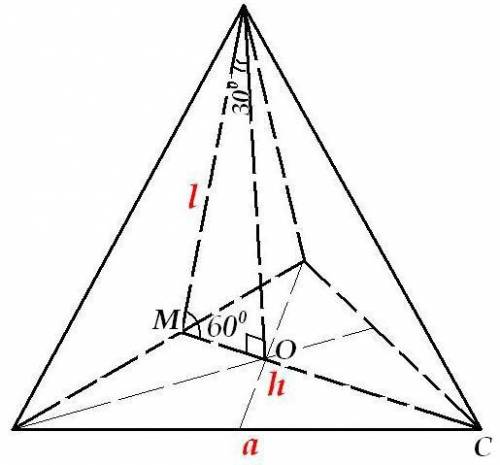
-сторона основания,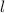 
- апофема, 
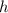- высота основания. Эти три величины потребуются для всего вычисления.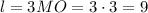
:
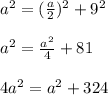
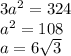
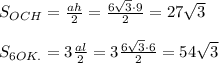
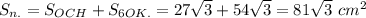
Противоположные углы попарно равны: ∠A = ∠C, ∠B = ∠D.
Диагонали делятся в точке их пересечения пополам: AO = OC, BO = OD.
Сумма соседних углов равна 180 градусов: ∠A + ∠B = 180, ∠B + ∠C = 180, ∠C + ∠D = 180, ∠D + ∠A = 180.
Противоположные стороны попарно равны и параллельны: AB = CD, AB || CD.
Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
Противоположные стороны попарно параллельны: AB || CD, AD || BC. 3) вроде у которого все стороны равны 4) Трапеция — четырёхугольник, у которого только одна пара противолежащих сторон параллельна. 6) Равнобедренная когда равны боковые стороны. Прямоугольная имеет прямой угол.