Дано: шар с центром в точке
R=13- радиус шара
плоскость а -сечение шара
р(а, О)=5 (расстояние от центра шара О до плоскости а
Найти: r-радиус круга в сечении
Решение
Сечением будет круг. Найдем его радиус. От центра шара до центра сечения 5 - это катет треугольника, который получится, если соединим центр шара, центр сечения и точку пересечения шара с его сечением. 13 - гипотенуза, по теорПифагора:r=√13²-5²=√144=12. S=πr²=π144=144πкв.ед
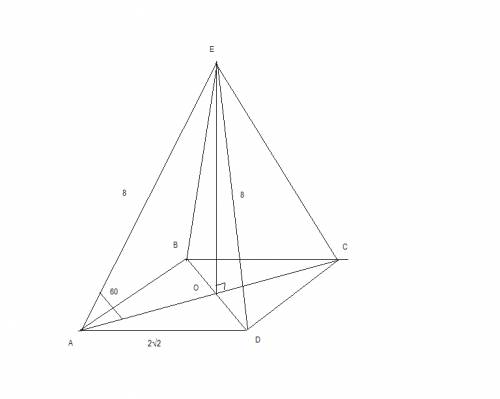
Боковое ребро правильной четырёхугольной пирамиды равняеться 8 см. и образует с площадью основания угол 60 градусов.Найти площадь боковой поверхности приамиды Sбок
правильная четырёхугольная пирамида -значит ABCD -квадрат
проекция AO бокового ребра AЕ на плоскость основания -это половина диагонали квадрата
АО=AЕ*cos60=8*1/2=4
треугольник АОD- прямоугольный АО=OD=4
гипотенуза AD= √(AO^2+OD^2)= √(4^2+4^2)= 2√2
рассмотрим треугольник AЕD
полупериметр р=(8+8+2√2)/2=8+√2
тогда по теореме Герона площадь треугольника
S(AЕD )= √[(8+√2)( 8+√2-8)( 8+√2-8)( 8+√2-2√2)]=2√31
площадь боковой поверхности приамиды Sбок= 4*S= 4*2√31 =8√31
ответ Sбок= 8√31
По теореме Пифагора АВ²=АС²+ВС²=15²+8²=225+64=289
АВ=17
Произведение секущей на её внешнюю часть есть число постоянное для данной точки.
AF·AK=AB·AD
7·23=17·AD
AD=7·23/17
BD=AB-AD= 17 - (7·23)/17=(289-161)/17=128/17
BD=128/17