Тема: "окружающая среда"
* * * для удобства плоскость (ABCD) обозначаем через Ψ * * *
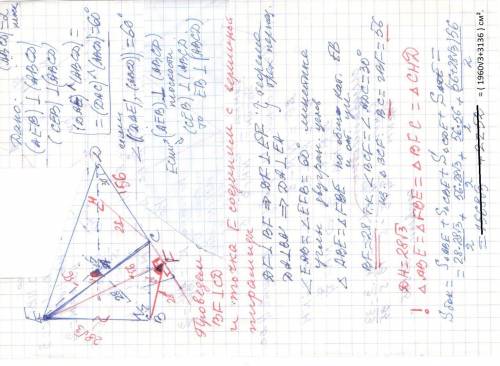
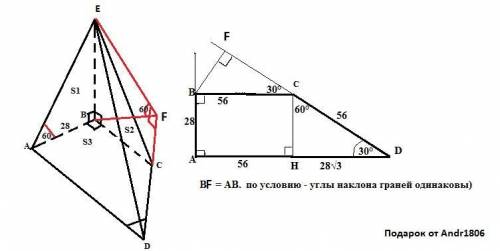
EABCD - пирамида , основание которой трапеция ABCD ;
AD || BC ; AB =28 ; ∠A =∠B =90° ; ∠D =30° ; | [AB] < [CD] ; [BC] < [AD]
(ABE) ⊥ Ψ и (CBE) ⊥ Ψ ; ∠ ( (CDE) , Ψ ) =∠ ( (ADE) , Ψ ) = 60°
--------------------------
1. Трапеция ABCD ПРЯМОУГОЛЬНАЯ
- - -
(ABE) ⊥ Ψ и (CBE) ⊥ Ψ ⇒ EB ⊥ Ψ
DA⊥ BA ⇒DA ⊥ EA ; ∠EAB =60° линейный угол двугранного угла
EADC ; Построим линейный угол двугранного угла EDCA
Проведем BF ⊥ CD и основание F этого перпендикуляра соединим с вершиной ПИРАМИДЫ E. Получаем ∠EFB = 60° линейный угол двугранного угла EDCA .
* * * ! ΔABE = ΔFBE =Δ BFC = ΔCHD учитывая ∠D =∠BCF =30° * * *
Вычисление площадей боковых граней и т.д. cм приложение
1)так как диагонали ромба точкой пересечения деляться пополам, то(рассматривая маленький треугольник-четверть ромба) один катет=8(16:2), а другой катет=15(30:2). по теореме Пифагора:
8*8+15*15=гипотенуза*гипотенуза
289=гипотенуза в квадрате
гипотенуза(или сторона ромба)=17
2)проведем высоту из не острого угла ромба.
получим маленький прямоугольный треугольник(равнобедренный)
по теореме Пифагора:
2а квадрат=64
а квадрат=32
а=корень из 32
а=4корня из 2
а(высота!)
S=8*4корня из 2
3)так как мы знаем что в равнобедренном треугольнике высота являеться медианой, отрезки АН=СН=8см
по теореме Пифагора:
36+64=100
ВС=АВ=10см
2) (В-С-А)->АС=АВ-ВС=14