Две прямые дороги KM и PN, которые пересекаются где-то за лесом в недоступной точке С. Нужно найти расстояние от некоторого пункта А на дороге КМ к точке С пересечения дорог. Для этого обозначили на дороге PN пункт В так, чтобы можно было измерить расстояние АВ, и определили углы ВАМ и ABN. Объясните нахождения расстояния АС. Вычислите АС, если АВ = 800 м , ∠ВАМ = 85°, ∠АВN = 52° .
Объяснение: Таким , зная определенные теоремы геометрии, можно не ходить часами с линейкой по дороге измеряя длину АС, а ВЫЧИСЛИТЬ ее по теореме синусов .
Теорема синусов :" Стороны треугольника пропорциональны синусам противолежащих углов."
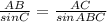. Видимый и измеряемый отрезок пути АВ=800 м. Угол ∠С вычисляется по т. о сумме углов треугольника, т.к два доступных угла можно измерить на местности с простейшей астролябии ( можно изготовить в домашних условиях) : ∠С=180°-85°-52°=43°.
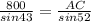, АС=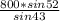 
≈ 
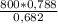≈ 924 (м).
1) используя т.Пифагора...
2) используя формулу для площади треугольника...
S = p*r, где р--полупериметр, r--радиус вписанной окружности
получается, что площадь прямоугольного треугольника = 5
радиусы вписанной в прямоугольный треугольник окружности отсекают на катетах квадрат)))
если обозначить оставшиеся части катетов (х) и (у) и вспомнить, что отрезки касательных, проведенных к окружности из одной точки, равны, то получим:
(х+1) + (у+1) + (х+у) = 10 --- периметр треугольника
2х + 2у = 8
х+у = 4
а площадь прямоугольного треугольника может быть вычислена как половина произведения катетов... S = 5 = (x+1)*(y+1) = xy + x + y + 1 = xy + 5
xy = 0 ---т.е. или х=0 или у=0 ---> треугольник не существует такой...