1—задача
O∈DE, DE||BC, DE - искомый отрезок
Радиус в точку касания перпендикулярен касательной.
Через точку можно провести только один перпендикуляр к прямой.
BC⊥AC => OE⊥AC => E - точка касания
△ADE~△ABC (по соответственным при DE||BC)
DE/BC =AE/AC => DE =3*3/4 =2,25 (см)
Объяснение:
Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
bananchikY
18 часов назад
Геометрия5 - 9 классы
ответ дан
1) В равнобедренном треугольнике, точка пересечения медиан отдалена от основания на 2a. Найдите расстояние от середины боковой стороны до основания.
2) Две стороны равнобедренного треугольника равны 15 см и 40 см. Найдите стороны подобного к нему треугольника, если его периметр составляет 190 см.
3) В равнобокой трапеции диагонали являются биссектрисами тупых углов. Расстояния от точки пересечения диагоналей к основаниям трапеции равны 2,25 см и 9,75 см. Найдите периметр трапеции, если средняя линия равна 8 см.
1
СМОТРЕТЬ ОТВЕТ
Войди чтобы добавить комментарий
Реклама
ответ
0
ant20202020
главный мозг
11.4 тыс. ответов
42.2 млн пользователей, получивших
1. ответ 3а, во вложении пояснения.
2. стороны в 15 см не могут быть боковыми сторонами, иначе 15+15<40 не выполняется неравенство треугольника, и значит, основание 15, а две боковые стороны по 40 см,
периметр подобного исходного треугольника равен 40+40+15=95, а периметр подобного 190, что в 2 раза больше , значит, каждая сторона подобного в два раза больше исходного. и тогда его стороны 15*2=30/см/, а две другие стороны по 40*2=80 см.
ответ 30см, 80 см, 80 см.
3. ответ (16+16√3) смво вложении пояснения.


1) Диагонали прямоугольника равны и точкой пересечения делятся пополам. Точка пересечения диагоналей прямоугольника - центр описанной окружности. Вершина пирамиды проецируется в центр описанной окружности основания, следовательно боковые ребра равны и составляют равные углы с плоскостью основания.
В прямоугольном треугольнике ABC отношение сторон 1:√3:2, AC=12. AO=AC/2=6
△AOK - равнобедренный прямоугольный, острые углы 45. Угол между плоскостью основания и боковыми ребрами 45.
2) Угол между прямой и плоскостью это угол между прямой и ее проекцией на плоскость.
AH⊥(a), AH=2√2
AH перпендикулярна плоскости и любой прямой в плоскости.
В прямоугольном треугольнике ACH
sin(ACH)=AH/AC =2√2/4 =√2/2 => ACH=60
△ABC - равнобедренный прямоугольный, отношение сторон 1:1:√2, AB=4√2
В прямоугольном треугольнике ABH
sin(ABH)=AH/AB =2√2/4√2 =1/2 => ABH=30
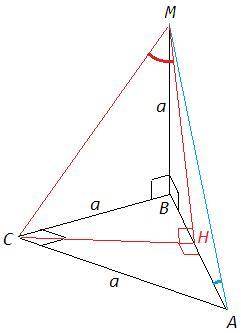
3) △ABC - равнобедренный прямоугольный, AB=a√2
В прямоугольном треугольнике MAB
tg(MAB)=MB/AB =a/a√2 =√2/2 => MAB= acrtg(√2/2) ~35,26
CH - высота и медиана в △ABC, CH=AB/2 =a√2/2
Плоскость (AMB) проходит через перпендикуляр к плоскости (ABC), следовательно (AMB)⊥(ABC). Прямая CH лежит в одной из перпендикулярных плоскостей и перпендикулярна линии их пересечения (CH⊥AB), следовательно CH⊥(AMB). MH - проекция MC на плоскость (AMB).
△MBC - равнобедренный прямоугольный, MC=a√2
В прямоугольном треугольнике CMH
sin(CMH)=CH/MC =a√2/2 : a√2 =1/2 => CMH=30
Во вписанных в окружность четырехугольниках сумма противоположных углов равна 180 градусов.
Поэтому угол АВС = 74 + 38 = 112
угол ADC = 180 - угол АВС = 180 - 112 = 68;
угол BCD = 180 - (угол DBC + угол BDC) = 180 - (38 + 65) = 77;
угол ВАС = 180 - угол BCD = 103;