Медиана треугольника делит его периметр пополам.докажите что треугольник равнобедренный

👇

Увидеть ответ

Ответ:

vladalogunova

22.02.2023

Пусть треугольник АВС, медиана ВМ

Согласно условию, периметры треугольников АВМ и ВМС равны.

Требуется доказать, что АВ=ВС

Доказательство:

1) Запишем равенство периметров треугольников: АВ+ВМ+АМ=ВМ+ВС+МС (1)

2) Так как, ВМ-медиана, то АМ=МС (2)

3)Учитывая равенства (1) и (2) запишем: АВ+ВМ+АМ= ВМ+ВС+АМ

4) Сокащаем ВМ и АМ в обеих частях равенства, получаем: АМ=ВС

Таким образом треугольник равнобедренный.

4,8(19 оценок)

Открыть все ответы

Ответ:

lizazarandiua

22.02.2023

Дано: ABCD - трапеция, 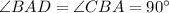$\angle BAD=\angle CBA=90^\circ$ , в ABCD вписана окружность l, точка К принадлежит l ( 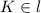$K\in l$ ), АК=20 см, KD=25 см.

Найти: 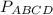$P_{ABCD}$

Решение: Пусть О - центр окружности l. Заметим, что диаметр окружности равен высоте трапеции. Построим перпендикуляр к стороне АВ от центра О окружности. Назовем его ОМ. Заметим, что АКОМ - квадрат. Все углы у него прямые, ОМ=ОК по построению. Значит ОК=АК=20 см. Значит АВ=2ОК=40 см.

По свойству четырехугольников, описанных вокруг окружности

AD+BC=AB+CD (*)

AD=AK+KD=20+25=45 см.

Подставим в (*) то, что известно

45+ВС=40+CD

BC=CD-5. (**)

Если из вершины С опустить высоту Т на основание AD, то можно рассмотреть прямоугольный треугольник CTD. CT=AB потому что, АВСТ - прямоугольник. Все углы прямые. Значит СТ=АВ=40 см. По построению TD=AD-AT=45-AT. AT=BC - по свойству прямоугольника. Пусть TD=x см.

Треугольник CTD - является прямоугольным по построению, так как 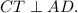$CT\perp AD.$

По теореме Пифагора

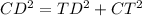
CD^2=TD^2+CT^2

Подставим известные данные и обозначения в последнюю формулу

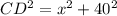
CD^2=x^2+40^2

Подставим CD в формулу (**)

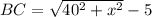
$BC=\sqrt{40^2+x^2}-5$

BC=AD-TD=45-x - подставляем в верхнюю формулу

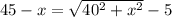
$45-x=\sqrt{40^2+x^2}-5$

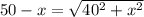
$50-x=\sqrt{40^2+x^2}$

Возведем в квадрат обе части

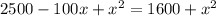
2500-100x+x^2=1600+x^2

2500-100x=1600

100x=2500-1600

100x=900

x=9 см

Значит TD=9 см, AT=AD-TD=45-9=36 cм. Так как по свойству прямоугольника АВСТ ВС=АТ=36 см.

Теперь осталось вычислить СD. По формуле (**)

36=СD-5

СD=36+5

СD=41 см.

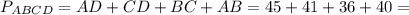
$P_{ABCD}=AD+CD+BC+AB=45+41+36+40=$

=86+36+40=122+40=162 см.

ответ: 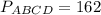$P_{ABCD}=162$ см

_________________________________________________________________________

Отвечаю на Ваш вопрос по решению примера по алгебре.

Упростим выражение

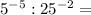
$5^{-5}:25^{-2}=$

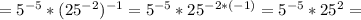
$=5^{-5}*(25^{-2})^{-1}=5^{-5}*25^{-2*(-1)}=5^{-5}*25^2=$

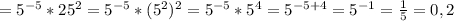
$=5^{-5}*25^2=5^{-5}*(5^2)^2=5^{-5}*5^4=5^{-5+4}=5^{-1}=\frac{1}{5}=0,2$

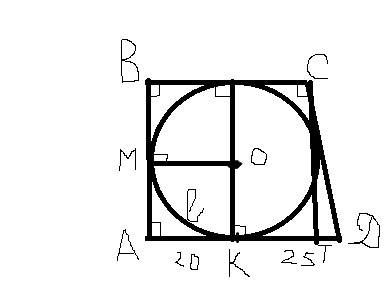
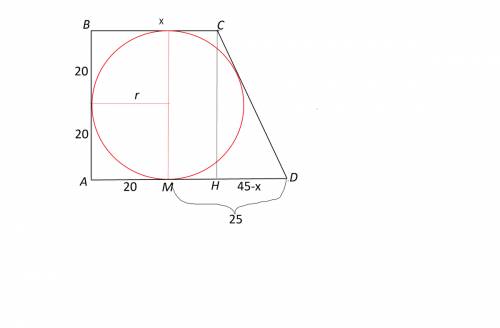
Точка касания окружности, вписанной в прямоугольную трапецию, делит ее большую основу для отрезки 20

4,6(86 оценок)

Ответ:

dgrigoref

22.02.2023

Сделаем рисунок к задаче.
Так как окружность вписана в трапецию, ее диаметр равен высоте трапеции, которая, в свою очередь, равна АВ ( т.к. углы А и В трапеции по условию равны 90°, и потому АВ равна высоте трапеции - расстоянию между ВС и АD)
Проведем диаметр трапеции через ее центр параллельно АВ.

Обозначим точку касания М ( диаметр перпендикулярен к касательной АД) .

АМ по условию равна 20 см.
Отсюда r=АМ=20 см,

D=Н= 40 см
AB=D=40 см.
Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы его противолежащих сторон равны.
Трапеция - четырехугольник, и т.к. в нее вписана окружность,
АВ+СD=ВС+АD.

АD=20+25=45 см
Пусть ВС =х
Тогда
СD=АD+ВС - АВ=45+х-40=х+5
Опустим из вершины С перпендикуляр СН на АД.
Получим прямоугольный треугольник СНД, в котором
СН=АВ=40 см
СD=х+5
НD=АD-ВС=45-х
Выразим из этого треугольника СД по т.Пифагора
СD²=СН²+НD²
(х+5)²=40²+(45-х)²
2025-90х+х²+1600=х²+10х+25
3600=100х
х=36
ВС=36 см
АD+ВС=45+36=81
АВ+СD=40+(36+5)=81
Периметр трапеции
Р=81+81=162 см