проведём высоту ДН.
т.к. АК и ДН высоты, значит АДНК-прямоугольник=>АД=КН=9 =>ВК=НС=(21-9)/2=6см
угол ВАК=135-90=45=>т.к. сумма углов в треугольнике равна 180=> уголАВК=45, значит треугольник АКВ-равнобедренный=>АК=ВК=6см
ответ:6см
8. <DBC=63°
9. P = 36 ед.
10. Не полное условие.
Объяснение:
Дуга BD равна 2*27° = 54° (так как вписанный угол, опирающийся на эту дугу, равен половине градусной меры этой дуги).
Дуга BDAC = 180°, так как ВС - диаметр.
Дуга DAC = DDAC - BD = 180-54 = 126°. =>
<DBC = 63° (вписанный, равен половине градусной меры дуги, на которую он опирается).
9. Биссектрисы углов параллелограмма отсекают от него равнобедренные треугольники. В нашем случае эти биссектрисы имеют общую точку Е на стороне ВС. Значит
АВ = ВЕ и EC = CD => BC = 2AB.
AB = СD и BC = AD (противоположные стороны параллелограмма).
Рabcd = 6*AB = 36 ед.
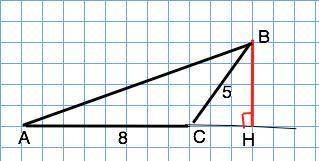
ответ:√137 (ед. длины)
Объяснение:
Площадь треугольника равна половине произведения высоты на сторону, к которой проведена. Тогда: Ѕ=а•h:2 ⇒ a•h=2S
Высота тупоугольного треугольника, проведенная из вершины острого угла, проходит вне треугольника и пересекает продолжение стороны, к которой проведена.
В ∆ АВС проведенная к стороне, равной 8 см, высота ВН=2•16:8=4. Тогда в "египетском" треугольнике ВСН отрезок СН=3 ( то же получим по т.Пифагора).
Треугольник АВН - прямоугольный, АН=8+3=11. По т.Пифагора его третья сторона АВ=√(АН²+BH²)=√(11²+4²)=√137
ак - перпендикуляр к бс и к ад угол бка = 90 градусов а угол бак = 135-90 (угол бад-угол каб(каб=90))=45 радусов значит в треугольнике бка угол к = 90 угол б=а=45 значит треугольник равнорбедренный и прямоугольный...
проведем с л=другой стороны высоту дн .. получается у нас получился прямоугольник кадн .. и кн=ад=9 значит бк+нс=21-9=12 а т.к. бк=нс то = 12/2=6 см
т.к. треугольник абк - равнобедренный то ак = бк = 6