5 - 9 классы 8+4 б
средняя линия равнобедренного треугольника, параллельная основанию, равна 3 см. найдите стороны треугольника, если его периметр равен 16 см.
отметить нарушение mrfoul 14.11.2012
ответ
проверено экспертом
ответ дан
ellenochka
ellenochka
по теореме осредней линии треугольника основание данного треугольника равно в 2 раза больше ср.линии: 3*2= 6 см
тогда общая длин двух других сторон 16 - 6 = 10 см
поскольку треугольник равнобедренный, то эти 2 стороны равны: 10/2 = 5 см
значит стороны треугольника равны : ребра по 5 см, а основание 6 см
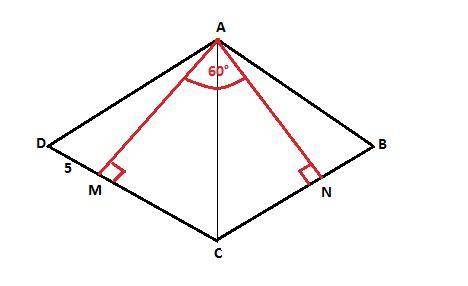
Pabcd = 40 дм.
Объяснение:
Прямоугольные треугольники DAM и BAN равны по гипотенузе и острому углу (гипотенузы DA и АВ - стороны ромба, ∠D = ∠B как противоположные углы ромба). Следовательно, ∠DAM = ∠BAN, а так как диагональ АС ромба делит ∠DAB пополам (свойство), то ∠MAC = <NAC = 30°. Тогда в прямоугольных треугольниках MAC и NAC ∠АСМ = ∠ACN = 60° (по сумме острых углов прямоугольного треугольника). Тогда угол ∠С ромба равен 120°, а ∠D = 60° (по сумме углов ромба, прилегающих к одной стороне).
В прямоугольном треугольнике DAM ∠ADM = 60°, ∠DAM=30°.
Против угла 30° лежит катет DM = 5 дм. Тогда гипотенуза DA (сторона ромба) равна 10 дм, а периметр ромба равен
10·4 = 40 дм.