7 см
Правильное условие:
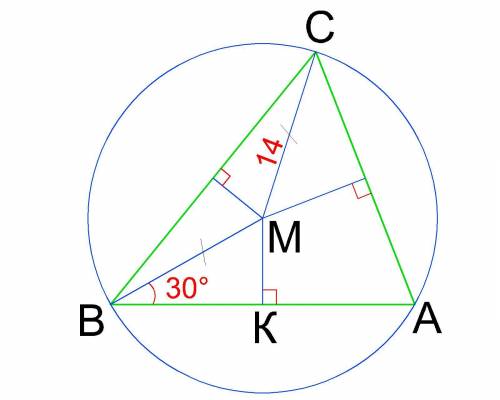
В остроугольном треугольнике ABC серединные перпендикуляры к сторонам BC и AC пересекаются в точке M. Известно, что MC = 14 см, ∠AВМ = 30°. Найдите расстояние от точки M до стороны AB. ответ дайте в сантиметрах.
Объяснение:
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке — центре описанной окружности.
Значит МА=МВ=МС=R = 14 см.
Тогда ΔАМВ - равнобедренный с основанием АВ и ∠МАВ=∠МВА=30°.
Расстоянием от т.М до стороны АВ есть высота равнобедренного ΔАМВ.
Построим высоту МК. Получили прямоугольный ΔВМК с прямым ∠МКВ и гипотенузой МВ.
Катет МК = sin∠MВK * MВ.
Т.к. ∠МВК = ∠АВМ = 30° и МА = 14 см, то
МК = sin 30° * 14 = 7 (см)
Если катеты одного прямоугольного треугольника соответственно равны катетам другого,то такие ттреугольники равны.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого,то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответсвенно равны гипотенузе и острому углу другого,то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответсвенно равны гипотенузе и катету другого, то такие треугольники равны.
РЕШЕНИЕ
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
-боковые ребра правильной пирамиды равны;
-все боковые грани — равные равнобедренные треугольники
высота пирамиды Н=l*sin(b)
основание пирамиды равносторонний треугольник
все углы равны - 60 град
все стороны равны -а
ВК - медиана, биссектриса, высота
ВО=l*cos(b)
BO=2/3*BK
BK=3/2*BO=3/2* l*cos(b)
сторона основания a =BK/sin60=3/2* l*cos(b)/(√3/2)= √3*l*cos(b)
высота боковой грани SM=√(SB^2-MB^2)=√(l^2-(a/2)^2)=√(l^2-((√3*l*cos(b))/2)^2)=
=1/2*l*√(4-3cos^2(b))
выразим ПЛОЩАДЬ треугольника SDB
- через ВЫСОТУ и ОСНОВАНИЕ двумя тогда имеем отношение BD*SM =SB*DF => DF= BD*SM /SB
h=DF=a* 1/2*l*√(4-3cos^2(b)) / l =√3*l*cos(b) *1/2*l*√(4-3cos^2(b)) / l=
=√3/2 *l*cos(b)√(4-3cos^2(b))
теорема косинусов
a^2 = h^2+h^2-2h^2*cosA =2h^2(1-cosA)
cosA=1 - a^2 / (2*h^2)
cosA =1- (√3*l*cos(b))^2 / (2*√3/2 *l*cos(b)√(4-3cos^2(b)))^2 = 1 - 1 / (4-3cos^(b))
A = arccos (1 - 1 / (4-3cos^(b)) )
ответ < A = arccos (1 - 1 / (4-3cos^(b)) ) ; Н=l*sin(b)