Задача 2 рисунок 1
Дано: ABC - прямоугольный равнобедренный треуг.
AD = 8 см - медиана
Найти: CB = ?
1) ABC - прямоугольный равнобедренный треуг.
угол А = 90 гр. => угол В + угол С = 90 гр.,
угол В = угол С (т.к. АВС равнобедренный) => угол В = угол С = 90/2 = 45 гр.
AD - высота, медиана и биссектриса (по свойству равнобедренного треуг.) => BD = CD
2) Рассмотрим треуг. ABD
угол D = 90 гр.
tg 45 = AD/BD => BD = AD/tg 45
BD = 8 см/1 = 8 см
3) CB = BD + CD = 8 + 8 = 16 см
ОТВЕТ: CB = 16 см
Задача 3 Рисунок 2
Дано: NMK - прямоугольный треуг.
NS = 10 см - медиана
угол M = 30 гр.
Найти: NK = ?
1) угол M + угол K = 90 гр (по свойству прямоугольного треуг.) =>
=> угол K = 90 - 30 = 60 гр
2) NS - медиана => MS = SK
3) NK = 1/2*MK (т.к. угол против 30 гр. равен половине гипотенузы) =>
=> NK = MS = SK
3) Рассмотрим треуг. NSK - равнобедренный треуг. (NK = SK)
угол K = 60 гр => угол S = угол N (т.к. углы при основании равны)
угол S = угол N = (180 - 60)/2 = 60
треуг. NSK - равносторонний => NK = NS = 10 см
ОТВЕТ: NK = 10 см
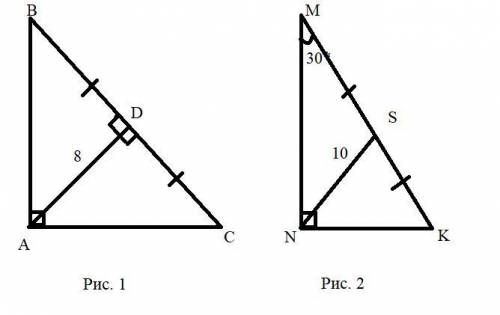
Задача 2 рисунок 1
Дано: ABC - прямоугольный равнобедренный треуг.
AD = 8 см - медиана
Найти: CB = ?
1) ABC - прямоугольный равнобедренный треуг.
угол А = 90 гр. => угол В + угол С = 90 гр.,
угол В = угол С (т.к. АВС равнобедренный) => угол В = угол С = 90/2 = 45 гр.
AD - высота, медиана и биссектриса (по свойству равнобедренного треуг.) => BD = CD
2) Рассмотрим треуг. ABD
угол D = 90 гр.
tg 45 = AD/BD => BD = AD/tg 45
BD = 8 см/1 = 8 см
3) CB = BD + CD = 8 + 8 = 16 см
ОТВЕТ: CB = 16 см
Задача 3 Рисунок 2
Дано: NMK - прямоугольный треуг.
NS = 10 см - медиана
угол M = 30 гр.
Найти: NK = ?
1) угол M + угол K = 90 гр (по свойству прямоугольного треуг.) =>
=> угол K = 90 - 30 = 60 гр
2) NS - медиана => MS = SK
3) NK = 1/2*MK (т.к. угол против 30 гр. равен половине гипотенузы) =>
=> NK = MS = SK
3) Рассмотрим треуг. NSK - равнобедренный треуг. (NK = SK)
угол K = 60 гр => угол S = угол N (т.к. углы при основании равны)
угол S = угол N = (180 - 60)/2 = 60
треуг. NSK - равносторонний => NK = NS = 10 см
ОТВЕТ: NK = 10 см

Опустим из В высоту ВН на АD.
По свойству равнобедренной трапеции высота, опущенная на большее основание, делит его на два отрезка, меньший из которых равен полуразности оснований.
АН=(52-12):2=20
Треугольник АВН, как видно, египетский, и ВН равна 15. По т.Пифагора
ВН=√(АВ-АН)=√(625-400)=15
Синус - отношение катета, противолежащего углу, к гипотенузе.
ВН- катет, АВ - гипотенуза.
sin (ВАН)=ВН:АН=15:25=0,6