ответ: 1 сторона=6см
2сторона=10см
3 сторона 14см
Р=30см
Объяснение: обозначим вершины треугольника А В С, пропорции 3: 5 : 7 как АВ=3х, ВС=5х, АС=7х и зная, что периметр треугольника составляет 60см составим уравнение:
3х+5х+7х=60
15х=60
х=60÷15
х=4
Теперь найжем каждую сторону треугольника:
1) АВ=3х=3×4=12см
2)ВС= 5х=5×4=20см
3) АС=7х=7×4=28см
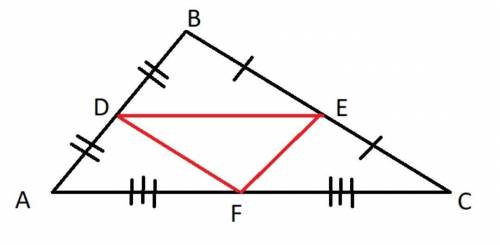
Так как треугольник DEF вписан в ∆АВС с середин сторон, то по правилам средней линии треугольника, средняя линия параллельная одной из его сторон равна половине этой стороны.
Поэтому EF || АВ и EF=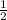
×AB =12÷2=6 см
DF || BC и EF=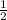×BC=20÷2=10см
DE || AC; DE=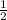×AC=28÷2=14см
тогда периметр второго треугольника составит: Р=6+10+14=30см
Дано:
тр АВС - р/б (АС - основание)
АМ, СК - медианы
АМ ∩ СК = О
Доказать:
тр АОК = тр СОМ
Доказательство:
1) Т.к тр АВС - р/ б и АМ и СК медианы по условию, то
а) АК=КВ=ВМ=МС
б) уг ВАС = уг ВСА (по св-ву углов при основании р/б тр)
2) тр АКС = тр СМА по двум сторонам и углу между ними, так как в них:
АС - общая сторона
АК = СМ (по п.1а)
уг КАС = уг МСА (по п.1б)
Следовательно, уг АКС = уг СМА и уг АСК = уг САМ
3) уг МАК = уг КСМ, как разность равных углов за минусом равных углов, по аксиоме измерения углов,
а именно уг МАК = уг ВАС - уг САМ и
уг КСМ = уг ВСА - уг АСК
4) Получили:
АК = СМ (из п 1а)
уг МАК = уг КСМ (из п 3)
уг АКС = уг СМА ( из п 2)
следовательно, тр АОК = тр СОМ по стороне и двум прилежащим к ней углам