
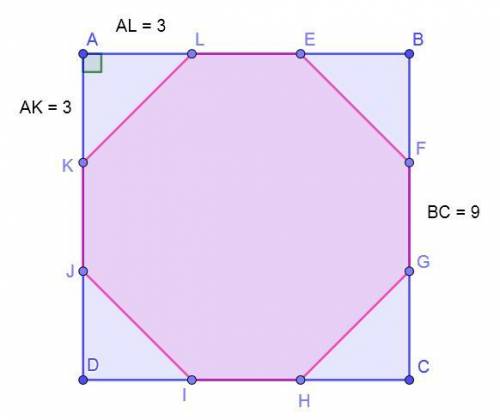
Внутри квадрата таким образом образовался 8-угольник и 4 равных равнобедренных прямоугольных треугольника с катетами 3.
Чтобы узнать площадь образовавшегося многоугольника, нужно от площади квадрата отнять сумму 4-х треугольников при вершинах квадрата.
Площадь квадрата:
S◻ = a² = 9² = 81 (кв. ед.)
Найдем площадь одного из треугольников^
SΔ = (ab)/2= (3·3)/2 = 9/2 (кв. ед.)
Найдем площадь 8-угольника:
S₈ = S◻ − SΔ = 81−(4·(9/2)) = 81−18 = 63 (кв. ед.)
ответ: Площадь образовавшегося многоугольника равна 63 кв. ед.
A(0;1) , B(2;5) , C(4 ;1) ; D(2; - 3) .
Док-ть четырехугольник ABCD ромб.
Объяснение:
Если диагонали четырехугольника взаимно перпендикулярны и точкой пересечения делятся пополам, то это ромб.
Координаты середины AC : O₁ (2 ;1 )
Координаты середины BD: O₂ (2 ;1 )
середины совпадают O₁ ≡ O₂
AC ( 4; 0) * * * (4-0 ; 1 - 1) * * *
BD ( 0 ; -8) * * * (2 -2 ; -3 -5) * * *
Скалярное произведения векторов AC и BD :
AC * BD = 4*0 +0*(-8) = 0 ⇒ AC ⊥ BD .