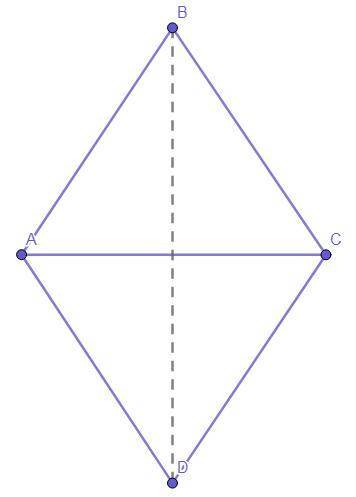
Четырёхугольник ABCD - ромб.
Отрезки АС и BD - диагонали.
АС = АВ.
Найти :Острый угол = ?
Решение :Ромб - это параллелограмм, у которого все стороны равны.
Поэтому -
АВ = ВС = CD = AD.
Рассмотрим ΔАВС.
АС = АВ = ВС.
Следовательно, ΔАВС - равносторонний (по определению равностороннего треугольника).
Каждый угол равностороннего треугольника равен по 60°.Отсюда -
∠ВАС = ∠В = ∠ВСА = 60°.
Диагональ ромба является биссектрисой его угла.То есть -
∠А = 60°*2 = 120°.
Противоположные углы параллелограмма равны.Следовательно -
∠В = ∠D = 60°
∠А = ∠С = 120°.
Отсюда острый угол ромба = 60°.
ответ :60°.
(Точки А и В делят окружность на дуги, которые относятся как 6:9, значит одна из образованных дуг соотвествует углу 360*6:(6+9)=144 градуса, а вторая 360*9:(6+9)=216 градусов
угол ВАС =216-180=36 градусов)
Решение
\\угол АВС, как угол опирающийся на диаметр равен 90 градусов
ответ: 90 градусов
прим. (???но тогда непонятно зачем делят окружность на дуги, которые относятся как 6:9)