Треугольник авс с основанием ас=8, угол а равен 60 градусов, ав=вс. найти площадь авс.

👇

Ответ:

milenkoInyashno

08.02.2021

В равнобедренном треугольнике углы при основании равны треугольнику САВ равен СВА, по первому признаку равенства треугольника СА=СВ=, СВ=СА, теперь пишем что допустим угол В=60 и тогда угол В+ угол А=60+60=120

4,7(11 оценок)

Открыть все ответы

Ответ:

овшаь

08.02.2021

Пусть дан треугольник АВС с прямым углом А, в котором проведена биссектриса АЕ, длину которой нужно найти.

Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.

Запишем пропорцию:

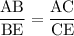
$\rm{\dfrac{AB}{BE}= \dfrac{AC}{CE}}$

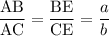
$\mathrm{\dfrac{AB}{AC}= \dfrac{BE}{CE}}=\dfrac{a}{b}$

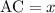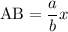Пусть $\mathrm{AC}=x$ . Тогда $\mathrm{AB}=\dfrac{a}{b} x$ .

Запишем теорему Пифагора для треугольника АВС:

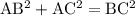
$\rm{AB^2+AC^2=BC^2}$

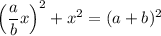
$\left(\dfrac{a}{b} x\right)^2+x^2=(a+b)^2$

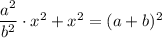
$\dfrac{a^2}{b^2}\cdot x^2+x^2=(a+b)^2$

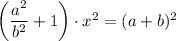
$\left(\dfrac{a^2}{b^2}+1\right)\cdot x^2=(a+b)^2$

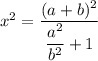
$x^2=\dfrac{(a+b)^2}{\dfrac{a^2}{b^2}+1}$

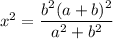
$x^2=\dfrac{b^2(a+b)^2}{a^2+b^2}$

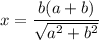
$x=\dfrac{b(a+b)}{\sqrt{a^2+b^2} }$

Значит:

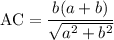
$\mathrm{AC}=\dfrac{b(a+b)}{\sqrt{a^2+b^2} }$

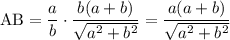
$\mathrm{AB}=\dfrac{a}{b}\cdot \dfrac{b(a+b)}{\sqrt{a^2+b^2} }=\dfrac{a(a+b)}{\sqrt{a^2+b^2} }$

Запишем теорему синусов для треугольника АЕС:

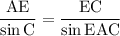
$\rm{\dfrac{AE}{\sin C} =\dfrac{EC}{\sin EAC} }$

Так как АЕ - биссектриса, то ЕАВ и ЕАС равны по половине прямого угла, то есть по 45°.

Синус угла С определим как отношение противолежащего катета к гипотенузе:

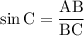
$\rm{\sin C=\dfrac{AB}{BC} }$

Теперь можем найти биссектрису:

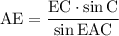
$\rm{AE =\dfrac{EC\cdot\sin C}{\sin EAC} }$

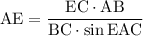
$\rm{AE =\dfrac{EC\cdot AB }{BC \cdot\sin EAC} }$

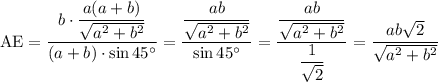
$\mathrm{AE} =\dfrac{b\cdot\dfrac{a(a+b)}{\sqrt{a^2+b^2} } }{(a+b) \cdot\sin 45^\circ}=\dfrac{\dfrac{ab}{\sqrt{a^2+b^2} } }{ \sin 45^\circ} }=\dfrac{\dfrac{ab}{\sqrt{a^2+b^2} } }{\dfrac{1}{\sqrt{2} } }=\dfrac{ab\sqrt{2}}{\sqrt{a^2+b^2}}$

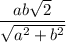
ответ: $\dfrac{ab\sqrt{2}}{\sqrt{a^2+b^2}}$

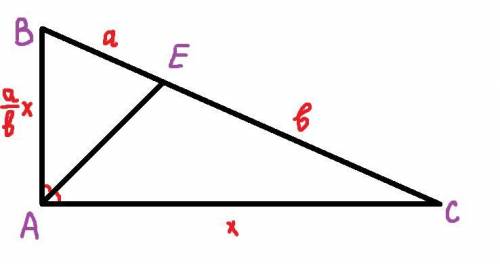
Из вершины прямого угла проведена биссектриса, делящая гипотенузу на отрезки а и b. Чему равна эта б

4,4(99 оценок)

Ответ:

Zauchka17

08.02.2021

Вписанные углы опирающиеся на диаметр равны по 90°, поэтому ∠ADC=90°=∠CBA.

Треугольник ADC - равнобедренный (DA=DC) и прямоугольный (∠ADC=90°), поэтому углы при его основании равны по 45°. ∠DAC=45°=∠DCA

Треугольник ABC - прямоугольный (∠CBA=90°), так же 2AB=AC. Угол лежащий напротив катета, который вдвое меньше гипотенузы равен 30°, поэтому ∠BCA=30°. Сумма острых углов в прямоугольном треугольнике составляет 90°, поэтому ∠BАС=60°.

∠BAD = ∠BAC+∠DAC = 60°+45° = 105°

∠BCD = ∠BCA+∠DCA = 30°+45° = 75°

ответ: ∠BAD=105°; ∠BСD=75°.

4,5(1 оценок)

Это интересно:

Кулинария-и-гостеприимство

02.02.2020

Как сделать красивые и вкусные французские макароны с миндалем...

Кулинария-и-гостеприимство

23.06.2020

Как заварить Кунг фу чай - лучший способ насладиться вкусом восточного чая...

Дом-и-сад