Відповідь:
Пояснення:
1. В прямокутному трикутнику один з кутів = 90°, а сума всіх кутів = 180°. Виходячи з цього невідомий кут х=180°-90°-47°=43°
Відповідь: 43°
2. Знайдемо суміжний кут зовнішнього кута 180°-117°=63°. В прямокутному трикутнику один з кутів = 90°, а сума всіх кутів = 180°. Виходячи з цього невідомий кут х=180°-90°-63°=27°
Відповідь: 63° та 27°
3. В цій задачі скористаємося теоремою Піфагора, щоб знайти другий катет:
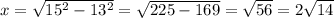
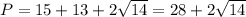 см
см
4. Оскільки із означення вписаного в коло прямокутного трикутника відомо, що радіус описаного кола дорівнює половині гіпотенузи, то гіпотенуза в даній задачі дорівнює відомому катету збільшеному в д рази.
Знайдемо кут протилежний відомому катету х:
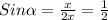
Один кут = 30°. Оскільки це прямокутний трикутник, то прямий кут = 90°, а третій кут = 180°-90°-30°=60°
Відповідь: кути трикутника 30°, 60°, 90°
5. Оскільки дотична із радіусом утворюють кут 90°, то утворюється прямокутний трикутник АОМ, в якому потрібно знайти гіпотенузу ОМ.
Третій кут в трикутнику буде дорівнювати 60°, оскільки 180°-90°-30°=60°.
За теоремою Синусів
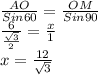
АВС, из условия имеем АВ = с, ВС = с/2, АС = 3с/4.
Найдем cos C:
cosC = (a^2+b^2-c^2) / (2ab) = (9/16 + 1/4 - 1)/(2*3/8) = - 1/4
(угол С - тупой). Тогда sin C = кор(1-cos^2 C) = (кор15)/4
По теореме синусов найдем sin A:
sin A = (a/c)sin C = (кор15)/8
По свойству биссектрисы вн. угла тр-ка (СО - биссектриса):
АО/ОВ = АС/СВ = 2/3
АО+ОВ = с Тогда: АО = 3с/5, ОВ = 2с/5
Проведем ОМ перп АС, ОМ - искомый радиус полукруга.
Из пр.тр. АОМ:
r = AO*sin A = (3c/5)*(кор15)/8 = (3с*кор15)/40.
ответ: r = (3с*кор15)/40.