ответ: Условие задачи – возможно, что намеренно – составлено некорректно.
Объяснение:
Если в параллелограмме известны стороны и высота, проведенная к одной из них, то длину второй высоты можно найти из его площади:
Ѕ=h•a, где h- высота, а - сторона, к которой она проведена.
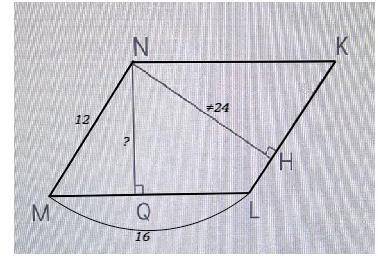
S=NH•KL => NQ=S:ML.
НО!
MNKL - параллелограмм, => NK=ML=16.
Тогда оказывается, что в ∆ NKH гипотенуза NK меньше катета NL ( 16 < 24), что противоречит отношению сторон прямоугольного треугольника.
1) В основаниях призмы лежат n-угольники. Основания призмы параллельны и равны. Количество вершин призмы равно количеству вершин n-угольников, лежащих в основаниях.
Количество вершин одного основания равно n. Т.к. оснований два и они равны, то количество вершин двух оснований равно 2n. Значит количество вершин в призме равно 2n.
2n это всегда четное число, т.к. оно делится. на 2. Значит число вершин любой призмы четно.
2) В основании призмы лежит n-угольник. Он имеет n сторон, которые являются ребрами призмы. В противоположном основании такой же n-угольник с точно таким же числом сторон.
Кроме этого все вершины одного основания соединены ребрами с соответствующими вершинами другого основания. Поскольку n пар вершин соединены ребрами, то ребер (боковых) тоже n штук.
Всего ребер у призмы n+n+n=3n.
Число 3n кратно 3. Следовательно число ребер любой призмы кратно 3.