а) y =-0,6x +13
б) 51/√34 ≈ 8,75 ед.
Объяснение:
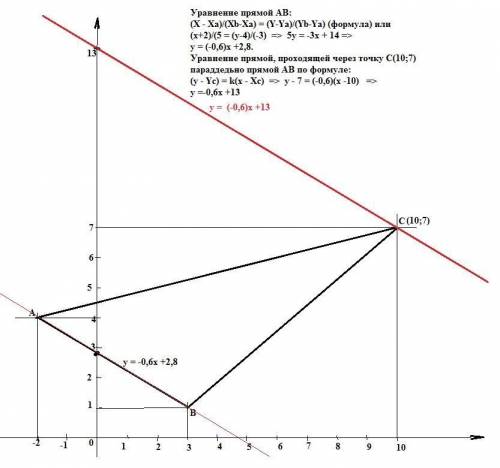
а). Уравнение прямой АВ:
(X - Xa)/(Xb-Xa) = (Y-Ya)/(Yb-Ya) (формула) =>
(x+2)/(5 = (y-4)/(-3) => 5y = -3x + 14 =>
y = (-0,6)x +2,8.
Уравнение прямой, проходящей через точку С(10;7) параллельно прямой АВ по формуле:
(y - Yc) = k(x - Xc) => y - 7 = (-0,6)(x -10) =>
y =-0,6x +13
б). Расстояние от точки М(Xm;Ym) до прямой Ax +By +C = 0 находится по формуле:
d = (A·Xm + B·Ym +C)/√(A²+B²).
В нашем случае уравнение прямой АВ: 3x + 5y - 14 =0.
Точка С(10:7). Тогда расстояние равно:
d = (3·10 +5·7 + (-14)/√(3²+5²) = 51/√34 ≈ 51/5,83 ≈ 8,75 ед.
Или так:
Площадь треугольника АВС, заданного координатами его вершин найдем по формуле:
S=(1/2)[(X1-X3)(Y2-Y3)-(X2-X3)(Y1-Y3)]. =>
S = (1/2)[(-2-10)(1-7)-(3-10)(4-7)] = 51/2 = 25,5.
Тогда высота СН к стороне АВ при модуле АВ, равном |AB| = √(5²+(-3)²) = √34:
СН = 2S/AB = 51/√34 ≈ 51/5,83 ≈ 8,75 ед.
Відповідь:
1757 жылдан Глазгодағы университетте механик болып жұмыс істеді. Онда ол Д.Папен (1647 – 1714) қазанын пайдаланып қаныққан бу температурасының қысымға тәуелділігін зерттеді. 1763 – 64 жылы Т.Ньюкоменнің (1663 – 1729) бу машинасының моделін кемелдендіре отырып, бу шығынын конденсаторды цилиндрден оқшаулау арқылы азайтуға болатындығын дәлелдеді. Осы идеяны басшылыққа ала отырып 1765 жылы тәжірибелік, ал 1768 жылы ең алғашқы бу машинасын құрастырды. Бұл бу машинасы Ньюкоменнің машиналарына қарағанда едәуір тиімді болды.
Пояснення:
периметры треугольников АВС и А'В'С' - РАВНЫ