Объяснение:
В условии не написано, чему данное выражение должно равняться, так распишу в общем случае и попытаюсь объяснить, как это делать.
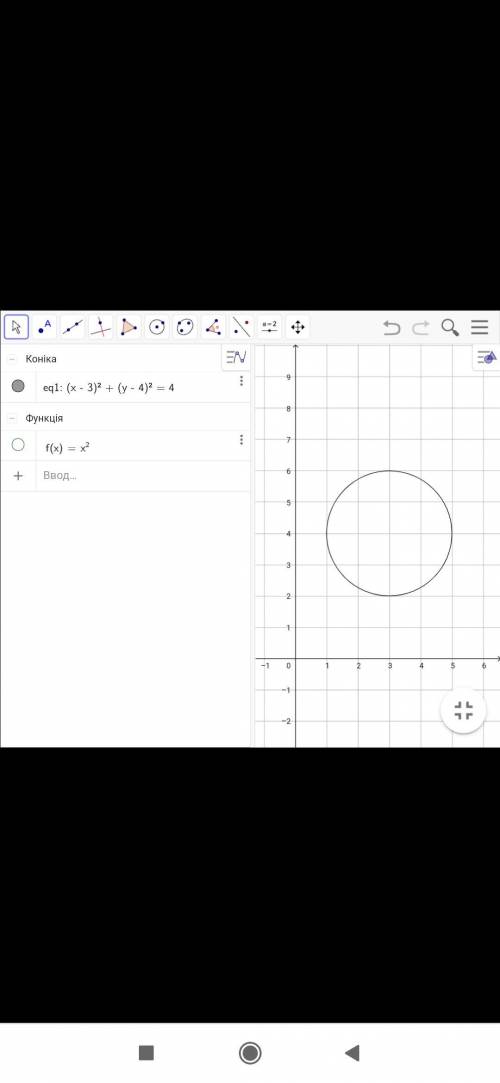
Есть общее уравнение окружности:
(х-а)²+(у-в)²=R², где а,в,R - заданные числа, х,у - переменные
Графиком данной функции будет окружность с центром в точке О
Как найти координаты данного центра?
Это всегда будет значения х и у, при которых в каждой из скобок (х-а)²+(у-в)² будет 0, то есть а и в
О(а;в)
А радиус это просто заданное число, так чтобы его найти, нужно извлечь корень из правой части √R²=|R|
К примеру, вот уравнение с графиком
Поскольку трапеция равнобедренная, то АН1=ЕН2. Найдем, чему равны эти отрезки:
АН1+Н1Н2+ЕН2=АЕ, но Н1Н2=ВС. Тогда
АН1+ВС+ЕН2=АЕ,
АН1+ЕН2=АЕ-ВС.
Поскольку АН1=ЕН2, выражение АН1+ЕН2=АЕ-ВС можно записать так:
АН1+АН1=АЕ-ВС
2АН1=АЕ-ВС
АН1=(АЕ-ВС):2, ЕН2=(АЕ-ВС):2
Найдем отрезок ЕН1:
ЕН1=Н1Н2+ЕН2=ВС+(АЕ-ВС):2
ЕН1=(ВС+АЕ):2