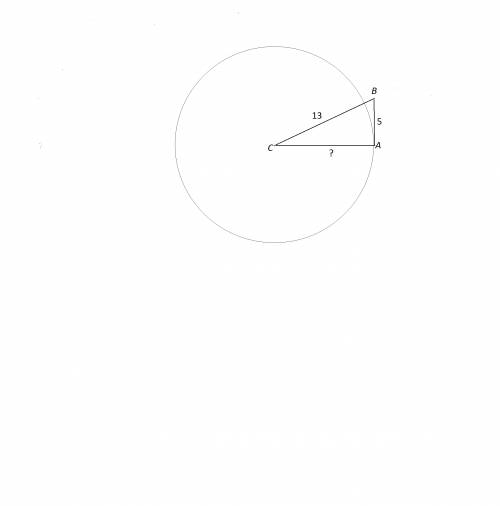
Если сделать рисунок, то будет понятно, что радиус этой окружности - катет АС данного прямоугольного треугольника.
Если окружность имеет с прямой только одну общую точку, то эта прямая - касательная к этой окружности.
Вершина угла А - точка касания.
Радиус окружности найдем по теореме Пифагора или вспомнив, что три стороны этого треугольника из так называемых троек Пифагора с отношением сторон 5:12:13.
------------------------------------------------------------------------------------------------------------------------------------
Треугольник, длины сторон которого равны пифагоровым числам, является прямоугольным. Кроме того, любой такой треугольник является героновым, то есть, все его стороны и площадь являются целыми числами.
----------------------------------------------------------------------------------------------------------------------------------------
Катет АС=12 см, и является радиусом данной окружности
Пусть АВ=3, АС=4 и ВС=5. Значит <C=90° и CosC=0. CosA=AC/AB (отношение прилежащего катета к гипотенузе) или CosA=3/5=0,6.
CosB=CB/AB или CosB=4/5=0,8.
ответ: CosA=0,6. CosB=0,8 и CosC=0.