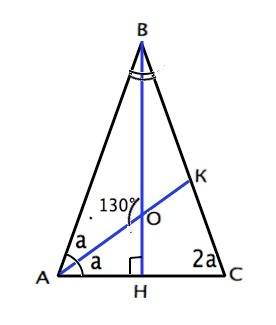
Один из углов, образованных при пересечении биссектрис угла при основании и угла при вершине равнобедренного треугольника, равен 130°. Найдите углы треугольника.
Пусть данный треугольник АВС, АВ=ВС, АК и ВН - биссектрисы, О - точка их пересечения. ∠ВАК=САК=а . Тогда ВСА=2а, т.к. углы при основании равнобедренного треугольника равны, а ∠ВНК=90° ( биссектриса при вершине равнобедренного треугольника еще и медиана и высота). В ∆ОАН из суммы смежных углов ∠АОН=180°-130°=50° , а из суммы углов треугольника ∠ОАН=180*-90°-50*=40°. ∠А=∠С=2•40*=80°. Из суммы углов треугольника находим ∠В=180°-2•80°=20°. Углы ∆АВС: 80°, 20°, 80°.
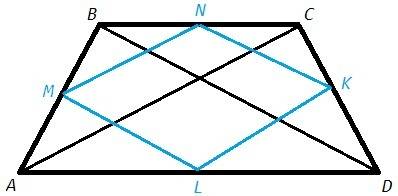
Середины сторон четырехугольника являются вершинами параллелограмма (теорема Вариньона). Стороны параллелограмма Вариньона параллельны диагоналям четырехугольника и равны их половинам (т.к. являются средними линиями в треугольниках, образованных сторонами и диагоналями).
Диагонали равнобедренной трапеции равны, следовательно стороны параллелограмма Вариньона равны и он является ромбом.
MN - средняя линия в ABC => MN||AC, MN=AC/2. Аналогично LK||AC, LK=AC/2.
MN||LK, MN=LK => MNKL - параллелограмм (противоположные стороны параллельны и равны).
AC=BD, NK=BD/2 => MN=NK => MNKL - ромб (смежные стороны равны).
2)Пусть треугольник АВС,АВ=2,С=60 градусов,Р-радиус окр,по теореме синусов получается
АВ/(синС)=2Р
2/(син60)=2Р
син60=
Р=
3)нет вопроса
4)Я считаю,что условие задачи не верно. Так как ВМ-медиана к АС,то АМ=МС,то есть углы,лежащие напротив них тоже равны,следовательно, угол АВМ=углу СВМ,а по условию АВМ больше СВМ,что невозможно