Для упрощения записей буду читать, что все ребра равны единице - все равно углы останутся прежними.
Введем ПСК с началом координат в центре нижнего основания (см. рисунок). Будем искать уравнения плоскостей. Уравнения имеют вид Xx+Yy+Zz=D.
Координаты точек:
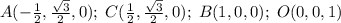
Плоскости a1 принадлежат точки B, C, O; поэтому ее уравнение находится из системы
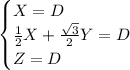
Решив систему, получаем уравнение плоскости
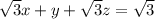
Аналогично, для второй плоскости
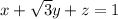
Отсюда получаем вектора нормалей для плоскостей:
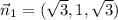
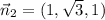
По формуле, можно найти косинус угла между плоскостями:
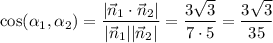
Искомый угол - арккосинус.
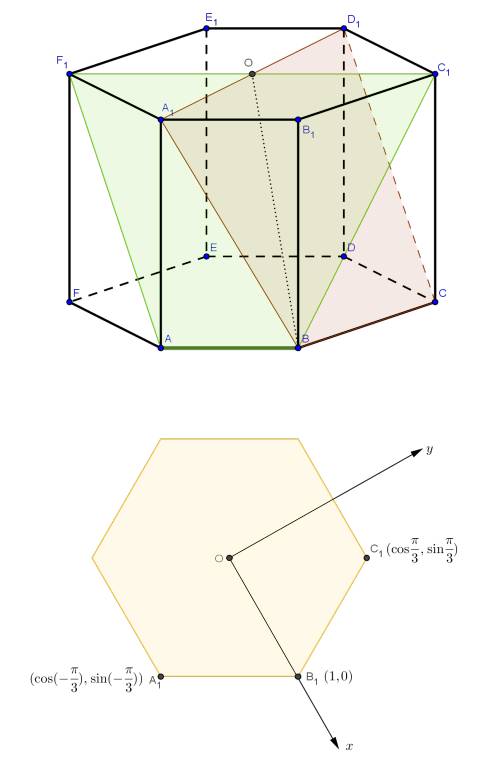

Рисунок смотри во вложении (чёрные линии лежат на плоскости, красные - вне плоскости).
Решение:
Опустим перпендикуляр АN из точки А на прямую СD. Точка N будет располагаться на продолжении стороны CD ромба. Проведем ЕN - расстояние от Е до прямой CD. ЕN =4 см по условию задачи.
Поскольку AN - перпендикуляр к CD, и АВ параллельно CD как стороны ромба, то <NAB - прямой. Значит, <NAD = <NAB - <DAB = 90 - 60 = 30
Рассмотрим треугольник AND:
АN = АD*cos30 = 4*(scrt{3}/2) = 2scrt{3}
Рассмотрим треугольник EAN. По теореме Пифагора найдем:
EА = scrt{EN^2 - AN^2} = scrt{4^2 - (2scrt{3})^2} = scrt{16 - 12} = 2
ответ: 2 см.
Выражение scrt{Х} обозначает квадратный корень из Х

Сделаем рисунок.
Очевидно, что треугольники АВС и А1В1С1 подобны.
Докажем это.
Прямые, которые пересекают плоскости α и β, образуют пересекающиеся прямые.
Через две пересекающиеся прямые можно провести плоскость. притом только одну.
Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
Следовательно, АВ||А₁В₁, ВС||В₁С₁, АС||А₁С₁
В каждой паре треугольников СОВ и С₁ОВ₁, АОВ и А₁ОВ₁, АОС и А₁ОС₁ соответственно углы равны.
Один - как вертикальный, два - как накрестлежащие при пересечении параллельных прямых секущей.
Если углы одного треугольника равны углам другого треугольника, зто такие треугольники подобны.
Отсюда следует подобие треугольников АВС и ,А₁В₁С₁, т.к. их стороны соответственно пропорциональны.
Итак, треугольники подобны.
В подобных треугольниках площади относятся как квадрат коэффициента подобия их линейных размеров.
Площадь треугольника АВС по формуле Герона равна 84 см² ( давать вычисления не буду, их можно сделать самостоятельно. Замечу, что такое отношение сторон треугольника встречается часто, и эту площадь многие знают наизусть.)
Найдем отношение площадей этих подобных треугольников.
S(ABC): S (A1B1C1)=336:84=4
k²=4
k=2
Следовательно, стороны треугольника А₁В₁С₁ в два раза больше сторон треугольника АВС и равны
А₁В₁=26 см
В₁С₁=28 см
А₁С₁=30 см
Для проверки можно вычислить по ф. Герона площадь треугольника А₁В₁С₁ получим 336 см²
—————
[email protected]