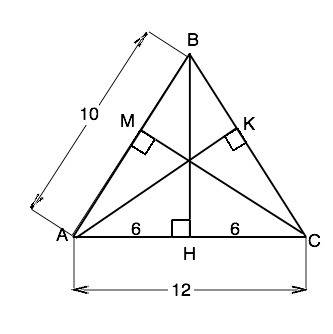
Дан треугольник, две стороны которого равны по 10 см, третья - 12 см. Этот треугольник равнобедренный. Обозначим его АВС, АВ=ВС. Проведем высоту ВН к основанию. Высота равнобедренного треугольника, проведенная к основанию, является его медианой. ⇒ АН=СН=6 см. По т.Пифагора ВН=√(АВ²-АН²)=√(100-36)=8 см. Высоты к боковым сторонам равнобедренного треугольника равны. Найдем их из площади ∆ АВС.
Ѕ(АВС)=АС•ВН:2=48 см² В то же время Ѕ(АВС)=СМ•АВ:2, поэтому СМ•10:2=48 см², откуда СМ=АК=96:10=9,6 см.
(5-2)*180=540°
Пусть углы пятиугольника будут 3х, 4х, 5х, 7х и 8х (раз они пропорциональны этим числам). Тогда
3х+4х+5х+7х+8х=540
27х=540
х=20
Искомые углы равны 3*20=60°, 4*20=80°, 5*20=100°, 7*20=140°, 8*2=160°
(60°+80°+100°+140°+160°=540°)