ответ: 1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
Объяснение: При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
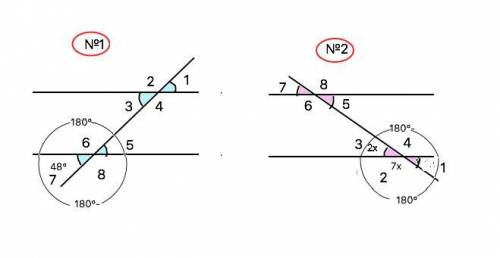
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
Нужно составить уравнения!
Обозначим стороны равнобедр. треугольника через Х,
основание - через У, медиану - через Р.
Имеем уравнения:
1. 2Х + У = 40 (периметр треуг. АВС) .
2. Х + 0,5У + Р = 33 (периметр треуг. АВМ) .
Умножив второе на 2, получим третье уравнение:
3. 2Х + У +2Р = 66.
2)Если длины боковых сторон равны х, а длина третьей стороны у, то возможны варианты:
а) 2х = 26 => x = 13
2х+у = 36 => y = 10
б) х+у = 26 => y = 26-x
2х+у = 36 => 2x + 26 - x = 36 => x = 10 => y = 16
Т. е. либо боковые стороны имеют длину 13, а третья - 10, либо боковые по 10, а третья - 16.
Р К, 26/2 = 13 : )
Вычтя из третьего - первое уравнение, найдем:
2Р = 26,
откуда Р= 13.
Итак, длина медианы Р=АМ равна 13 см.
Пояснения:
В первом уравнении стоит 2Х, т. к. треугольник равнобедренный, т. е. 2 стороны равны!
Во втором уравнении стоит 0,5У, т. к. медиана проводится к середине, в данном случае - к средине основания.