Уже встречалась эта задача. И решала я ее не так давно.
Задача на подобие треугольников и теоремы о параллельных плоскостях и прямых.
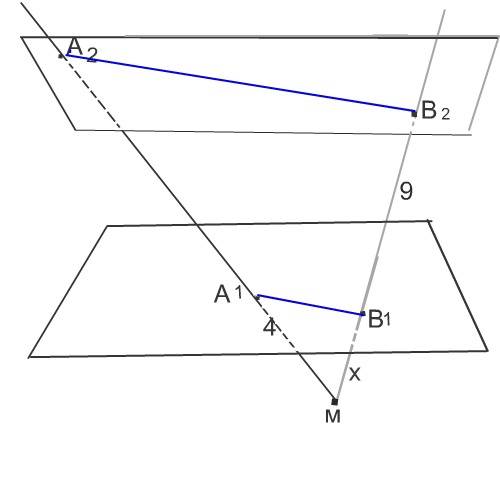
Проведем через точку М, А2 и В2 плоскость.
А1В1 параллельна А2В2 как линии пересечения параллельных плоскостей третьей плоскостью.
Остюда треугольники МА2В2 и МА1В1 подобны.
Примем отрезок МВ1 за х
Тогда МВ2=9+х,
МА2=9+х+4
4:(13+х)=х:(9+х)
36+4х=13х+х²
х²+9х-36=0
При необходимости полное решение квадратного уравнения запишете самостоятельно, а корни его 3 и -12. Второй корень не подходит.
х=3 см
МВ2=9+3=12 см
МА2=12+4=16 см
Задача на подобие треугольников и теоремы о параллельных плоскостях и прямых.
Проведем через точку М, А2 и В2 плоскость.
А1В1 параллельна А2В2 как линии пересечения параллельных плоскостей третьей плоскостью.
Остюда треугольникиМА2В2 и МА1В1подобны.
Примем отрезок МВ1 за х
Тогда МВ2=9+х,
МА2=9+х+4
4:(13+х)=х:(9+х)
36+4х=13х+х²
х²+9х-36=0
При необходимости полное решение квадратного уравнения запишете самостоятельно, а корни его 3 и -12. Второй корень не подходит.
х=3 см
МВ2=9+3=12 см
МА2=12+4=16 см
Пусть SABC - правильная треугольная пирамида, О - центр основания,
SD - апофема.
Обозначим сторону основания через Х, а боковую сторону через Y.
Тогда по теореме Пифагора
SD² = Y² - (X/2)² = Y² - X²/4 = 225
SO² = Y² - (X/√3)² = Y² - X²/3 = 144
Отняв уравнения, получаем Х² / 12 = 81 , откуда Х² = 972 или Х = 18 * √3
Тогда Y² = 225 + (18 * √3)²/4 = 225 + 243 = 468 ,
а Y = √ 468 = 6 * √13